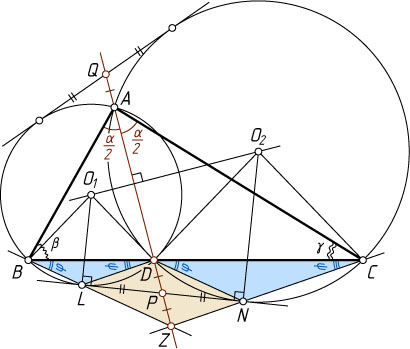
13623. Отрезок AD
— биссектриса треугольника ABC
. Прямая AD
пересекает общие касательные к описанным окружностям треугольников ABD
и ACD
в точках P
и Q
. Докажите, что PQ^{2}=AB\cdot AC
.
Решение. Обозначим \angle BAC=\alpha
, \angle ABC=\beta
, \angle ACB=\gamma
. Пусть O_{1}
и O_{2}
— центры, а R_{1}
и R_{2}
— радиусы описанных окружностей треугольников ABD
и ACD
соответственно, точки D
и P
расположены в одной полуплоскости относительно прямой O_{1}O_{2}
, а L
и N
соответственно — точки касания окружностей с их общей касательной, содержащей точку P
. Тогда P
— середина отрезка LN
(см. задачу 444). Точки A
и D
, а также P
и Q
симметричны относительно прямой O_{1}O_{2}
, поэтому AQ=DP
.
Равнобедренные треугольники BO_{1}D
и DO_{2}C
имеют углы при вершинах, равные \alpha
, следовательно, они подобны, т. е. \frac{BD}{DC}=\frac{R_{1}}{R_{2}}
. Кроме того, O_{1}B\parallel O_{2}D
и O_{1}D\parallel O_{2}C
. Поскольку O_{1}L\perp LN
и O_{2}N\perp LN
, то O_{1}L\parallel O_{2}N
. Значит, подобны треугольники BO_{1}L
и DO_{2}N
, а также треугольники LO_{1}D
и NO_{2}C
. Поэтому \frac{BL}{DN}=\frac{R_{1}}{R_{2}}=\frac{LD}{CN}
.
Отношения соответственных сторон треугольников BLD
и DNC
равны, следовательно, они подобны. Обозначим \angle LBD=\angle NDC=\varphi
, \angle LDB=\angle NCD=\psi
. Из треугольника BDL
и вписанного четырёхугольника ABLD
получаем: \varphi+\psi=180^{\circ}-\angle BLD=\frac{\alpha}{2}
.
Пусть прямые BL
и CN
пересекаются в точке Z
. Поскольку LZ\parallel DN
(обе эти прямые образуют угол \varphi
с прямой BC
) и NZ\parallel DL
(обе эти прямые образуют угол \psi
с прямой BC
), то LDNZ
— параллелограмм. Поскольку P
— середина его диагонали LN
, то прямая PQ
проходит через точку Z
, причём PZ=DP=AQ
. Значит, PQ=AZ
.
Рассмотрим треугольник ABZ
. Его угол при вершине B
равен \beta+\varphi
; угол при вершине A
равен \frac{\alpha}{2}
. Так как \varphi+\psi=\frac{\alpha}{2}
, то его угол при вершине Z
равен
180^{\circ}-(\beta+\varphi)-\frac{\alpha}{2}=180^{\circ}-\beta-\left(\frac{\alpha}{2}-\psi\right)-\frac{\alpha}{2}=\gamma+\psi.
Значит, он подобен треугольнику AZC
, т. е. \frac{AB}{AZ}=\frac{AZ}{AC}
, откуда AB\cdot AC=AZ^{2}=PQ^{2}
.
Источник: Журнал «Crux Mathematicorum». — 1999, № 3, задача 2336 (1998, с. 177), с. 191
