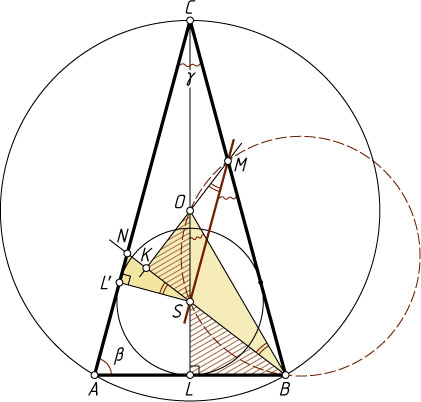
13710. Точка M
лежит на боковой стороне BC
равнобедренного треугольника ABC
с основанием AB
. Точки O
и S
— центры соответственно описанной и вписанной окружностей треугольника ABC
. Докажите, что SM\parallel AC
тогда и только тогда, когда OM\perp BS
.
Решение. Рассмотрим случай, изображённый на рисунке. Для остальных случаев решение аналогично.
Обозначим \angle A=\angle B=\beta
, \angle C=\gamma
. Пусть прямая BS
пересекает прямые MO
и AC
в точках K
и N
соответственно, а вписанная окружность треугольника ABC
касается сторон AB
и AC
в точках L
и L'
соответственно. Треугольник ABC
равнобедренный, поэтому точки C
, O
, S
и L
лежат на одной прямой (содержащей высоту треугольника ABC
).
Заметим, что луч BS
— биссектриса угла ABC
. Тогда
\angle OBS=\angle ABO-\angle ABS=(90^{\circ}-\angle BOL)-\frac{1}{2}\angle ABC=
=(90^{\circ}-\gamma)-\frac{\beta}{2}=\left(\beta+\frac{\gamma}{2}-\gamma\right)-\frac{\beta}{2}=\frac{\beta-\gamma}{2},
а так как
\angle NSL'=90^{\circ}-\angle SNL'=90^{\circ}-(\angle BCN+\angle CBN)=
=90^{\circ}-\gamma-\frac{\beta}{2}=\beta+\frac{\gamma}{2}-\gamma-\frac{\beta}{2}=\frac{\beta-\gamma}{2},
то \angle OBS=\angle NSL'
.
Необходимость. Пусть SM\parallel AC
. Тогда
\angle SMB=\angle ACB=\gamma=\angle SOB,
поэтому четырёхугольник SOMB
вписанный (см. задачу 12). Значит, \angle OMS=\angle OBS
. Тогда
\angle OMB=\angle OMS+\angle SMB=\angle OBS+\angle SMB=\frac{\beta-\gamma}{2}+\gamma=\frac{\beta+\gamma}{2}.
Из вписанности четырёхугольника SOMB
получаем
\angle KOS+\angle OSK=\angle SBM+\angle OMB=\frac{\beta}{2}+\frac{\beta+\gamma}{2}=\beta+\frac{\gamma}{2}=90^{\circ}.
Следовательно, OM\perp BS
. Необходимость доказана.
Достаточность. Пусть OM\perp BS
. Поскольку \angle OBS=\angle NSL'
, прямоугольный треугольник OKB
подобен прямоугольному треугольнику NL'S
. Кроме того, прямоугольный треугольник OKS
подобен прямоугольному треугольнику BLS
. Значит,
\frac{NS}{SL}=\frac{NS}{SL'}=\frac{OB}{KB}=\frac{CO}{KB},~\frac{SL}{SB}=\frac{SK}{OS}.
После умножения получаем
\frac{NS}{SB}=\frac{NS}{SL}\cdot\frac{SL}{SB}=\frac{CO}{KB}\cdot\frac{SK}{OS}=\frac{CM}{MB},
так как по теореме Менелая для треугольника CSB
и прямой MK
получаем, что
\frac{CM}{MB}\cdot\frac{BK}{KS}\cdot\frac{SO}{OC}=1,
откуда
\frac{CM}{MB}=\frac{KS}{BK}\cdot\frac{OC}{SO}=\frac{CO}{KB}\cdot\frac{SK}{OS}.
Из равенства \frac{NS}{SB}=\frac{CM}{MB}
следует, что MS\parallel CN
, т. е. MS\parallel AC
. Что и требовалось доказать.
Источник: Журнал «Crux Mathematicorum». — 2002, № 8, задача 2, с. 486
Источник: Математические олимпиады Боснии и Герцеговины. — 1997
