13732. Докажите, что две стороны выпуклого многоугольника, не имеющие общих концов, не могут обе быть больше наибольшей диагонали.
Решение. Пусть AB
и CD
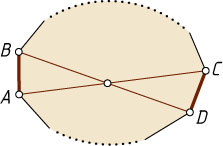
— две не имеющие общих концов стороны выпуклого многоугольника (см. рис.). Поскольку многоугольник выпуклый, то диагонали AC
и BD
пересекаются в точке, лежащей внутри него. Тогда сумма двух противоположных сторон выпуклого четырёхугольника ABCD
меньше суммы его диагоналей (см. задачу 3516). Значит,
AB+CD\lt AC+BD\leqslant2d,
где d
— длина наибольшей диагонали данного многоугольника. Следовательно, слагаемые AB
и CD
не могут оба быть больше d
. Что и требовалось доказать.
Источник: Журнал «Crux Mathematicorum». — 2004, № 3, задача 2831 (2003, с. 176), с. 183
