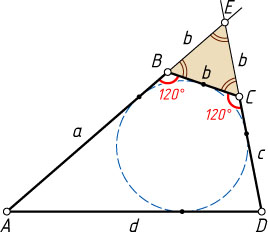
13739. В выпуклом четырёхугольнике ABCD
известно, что \angle ABC=\angle BCD=120^{\circ}
, а AB^{2}+BC^{2}+CD^{2}=AD^{2}
. Докажите, в этот четырёхугольник можно вписать окружность.
Решение. Обозначим AB=a
, BC=b
, CD=c
, AD=d
. Пусть E
— точка пересечения прямых AB
и CD
. Тогда треугольник BEC
с углами 60^{\circ}
при вершинах B
и C
— равносторонний. Значит,
BE=BC=CE=b.
По теореме косинусов из треугольника AED
получаем
d^{2}=(a+b)^{2}+(b+c)^{2}-(a+b)(c+a)=a^{2}+b^{2}+c^{2}+ab+bc-ac=
=d^{2}+ab+bc-ac,
откуда
ab+bc-ac=0.
Тогда
d^{2}=a^{2}+b^{2}+c^{2}=a^{2}+b^{2}+c^{2}-2(ab+bc-ac)=
=a^{2}+b^{2}+c^{2}-2ab-2bc+2ac=(a+c-b)^{2}.
Значит, либо d=a+c-b
, либо d=b-a-c
. Последнее равенство невозможно, так как d\gt b
, поэтому d=a+c-b
, или a+c=b+d
. Следовательно, четырёхугольник ABCD
описанный (см. задачу 364).
Источник: Журнал «Crux Mathematicorum». — 2004, № 5, задача 2849 (2003, с. 242), с. 301
