13744. Точки I
, O
и G
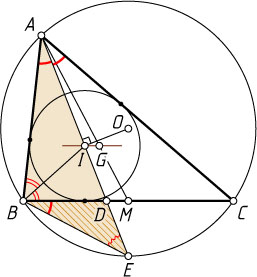
— соответственно центр вписанной окружности, центр описанной окружности и точка пересечения медиан треугольника ABC
. Известно, что \angle AIO=90^{\circ}
. Докажите, что IG\parallel BC
.
Решение. Пусть M
— середина стороны BC
треугольника ABC
, а биссектриса AI
угла BAC
пересекает сторону BC
и описанную окружность в точках D
и E
соответственно. Тогда AG:GM=2:1
.
Поскольку AI
— биссектриса угла ABC
, а вписанные углы CBE
и CAE
опираются на одну и ту же дугу, то
\angle BAE=\angle BAI=\angle IAC=\angle CAE=\angle CBE=\angle DBE.
По теореме о трилистнике (см. задачу 788) BE=EI
, а треугольники ABE
и BDE
с общим углом при вершине E
подобны по двум углам. Значит,
AB:BD=AE:BE=AE:EI.
Поскольку OI\perp AE
, то I
— середина хорды AE
(см. задачу 1676), поэтому
AB:BD=AE:EI=2:1.
Кроме того, по свойству биссектрисы треугольника (см. задачу 1509)
AI:ID=AB:BD=2:1.
Значит, AI:ID=AG:GM
. Следовательно, IG\parallel BC
. Что и требовалось доказать.
Примечание. Можно доказать, что оба условия (\angle AIO=90^{\circ}
и IG\parallel BC
) равносильны тому, что треугольник ABC
разностный (см. 6100).
Источник: Журнал «Crux Mathematicorum». — 2004, № 6, задача 2870 (2003, с. 399), с. 382
