1375. Докажите, что площадь прямоугольного треугольника с острым углом в 15^{\circ}
равна одной восьмой квадрата гипотенузы.
Указание. Проведите медиану из вершины прямого угла.
Решение. Пусть ABC
— данный прямоугольный треугольник,
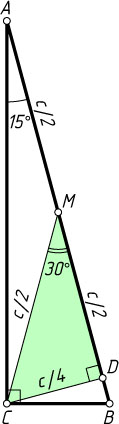
\angle C=90^{\circ},~\angle A=15^{\circ},~AB=c.
Проведём медиану CM
. Тогда (см. задачу 1109)
CM=BM=AM=\frac{1}{2}AB=\frac{c}{2},~\angle BMC=\angle A+\angle ACM=15^{\circ}+15^{\circ}=30^{\circ}.
Пусть CD
— высота треугольника BCM
. Тогда из прямоугольного треугольника CDM
находим, что
CD=\frac{1}{2}CM=\frac{c}{4}.
Следовательно,
S_{\triangle ABC}=\frac{1}{2}AB\cdot CD=\frac{c^{2}}{8}.
Источник: Куланин Е. Д., Федин С. Н. Геометрия треугольника в задачах: Экспериментальное учебное пособие для 8—10 кл. школ физико-математического направления. — М.: НИИ школ, 1990. — № 34, с. 33
