13765. Вне прямоугольного треугольника ABC
на его катетах AC
и AB
и гипотенузе BC
построены квадраты ACDE
, BAFG
и CBIJ
; AH
— биссектриса треугольника EAF
, а точка A'
, лежащая вне квадрата CBIJ
, — вершина прямого угла прямоугольного треугольника A'JI
, равного треугольнику ABC
. Докажите, что четырёхугольник A'DHG
вписанный.
Решение. Заметим, что точки D
, A
и G
лежат на одной прямой (содержащей биссектрису угла BAF
), а также точки H
, A
и A'
лежат на одной прямой (содержащей биссектрису угла EAF
).
Обозначим AC=b
, AB=c
. Пусть прямые AB
и A'I
пересекаются в точке S
, а прямые AC
и A'J
— в точке T
. Тогда ATA'S
— квадрат со стороной b+c
и диагональю A'A=(b+c)\sqrt{2}
, а AE=b
, AF=c
, DA=b\sqrt{2}
и AG=c\sqrt{2}
.
По формуле для биссектрисы треугольника (см. задачу 4021)
AH=\frac{2bc\cos45^{\circ}}{b+c}=\frac{bc\sqrt{2}}{b+c}.
Тогда
DA\cdot AG=b\sqrt{2}\cdot c\sqrt{2}=2bc,
A'A\cdot AH=(b+c)\sqrt{2}\cdot\frac{bc\sqrt{2}}{b+c}=2bc.
Значит, DA\cdot AG=A'A\cdot AH
, поэтому (см. задачу 114) точки A'
, D
, H
и G
лежат на одной окружности. Следовательно, четырёхугольник A'DHG
вписанный. Что и требовалось доказать.
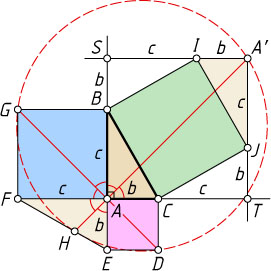
Источник: Журнал «Crux Mathematicorum». — 2005, № 6, задача 2958 (2004, с. 297, 300), с. 402
