13896. Дан неравнобедренный прямоугольный треугольник ABC
с прямым углом при вершине A
. Касательная в точке A
к его описанной окружности пересекает прямую BC
в точке M
. Вписанная окружность треугольника ABC
касается катетов AB
и AC
в точках R
и S
соответственно, а прямая RS
пересекает прямую BC
в точке N
. Докажите, что треугольник UMN
равнобедренный.
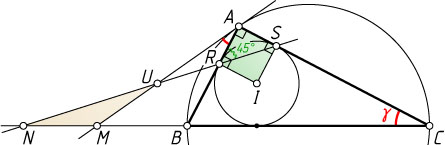
Решение. Рассмотрим случай, когда точка M
лежит на продолжении гипотенузы за точку B
(см. рис.).
Пусть I
— центр вписанной окружности треугольника ABC
. Тогда четырёхугольник ARIS
— квадрат, поэтому \angle ARS=45^{\circ}
Обозначим \angle ACB=\gamma
. Из теоремы об угле между касательной и хордой (см. задачу 87) получаем, что
\angle UAR=\angle MAB=\angle ACB=\gamma.
Тогда по теореме о внешнем угле треугольника
\angle MUN=\angle AUR=\angle ARS-\angle UAR=45^{\circ}-\gamma,
\angle UMN=\angle AMN=\angle CAM+\angle ACM=(\angle CAB+\angle MAB)+\angle ACM=
=(90^{\circ}+\gamma)+\gamma=90^{\circ}+2\gamma.
Значит,
\angle UNM=180^{\circ}-\angle MUN-\angle UMN=180^{\circ}-(45^{\circ}-\gamma)-(90^{\circ}+2\gamma)=
=45^{\circ}-\gamma=\angle MUN.
Следовательно, треугольник UMN
равнобедренный, MU=MN
. Что и требовалось доказать.