13933. Точка M
— середина не содержащей вершину A
дуги описанной окружности треугольника ABC
. Прямая, проведённая через точку M
перпендикулярно AB
, и прямая, проведённая через через точку B
перпендикулярно BM
, пересекаются в точке K
, а прямая, проведённая через точку M
перпендикулярно AC
, и прямая, проведённая через через точку C
перпендикулярно CM
, пересекаются в точке L
. Докажите, что прямые BC
и AM
пересекаются в середине отрезка KL
.
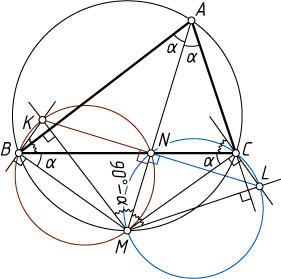
Решение. Рассмотрим случай, изображённый на рисунке. Поскольку M
— середина не содержащей вершину A
дуги описанной окружности треугольника ABC
, то AM
— биссектриса угла BAC
.
Обозначим \angle BAM=\angle CAM=\alpha
. Пусть N
— точка пересечения AM
и BC
. Вписанные углы CAM
и CBM
опираются на одну и ту же дугу, поэтому
\alpha=\angle BAM=\angle CAM=\angle CBM,
а так как KM\perp AB
и MB\perp BK
, то
\angle NMK=\angle AMK=90^{\circ}-\alpha~\mbox{и}~\angle NBK=\angle MBK-\angle MBC=90^{\circ}-\alpha.
Из точек B
и M
, лежащих по одну сторону от прямой KN
, отрезок KN
виден под одним и тем же углом, значит, точки B
, M
, N
и K
лежат на одной окружности (см. задачу 12), а так как \angle KBM=90^{\circ}
, то отрезок KM
— диаметр этой окружности. Значит, \angle KNM=90^{\circ}
. Аналогично, \angle LNM=90^{\circ}
, следовательно, точки K
, N
и L
лежат на одной прямой.
Прямоугольные треугольники KNM
и LNM
равны по общему катету MN
и прилежащему острому углу, поэтому KN=NL
, т. е. N
— середина отрезка KL
. Отсюда следует утверждение задачи.
Аналогично для любого другого случая.
Источник: Журнал «Crux Mathematicorum». — 2013, № 6, задача 3756 (2012, с. 242, 244), с. 282
