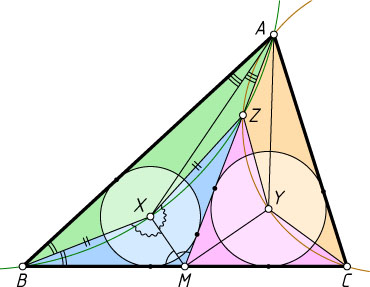
13991. На стороне BC
треугольника ABC
отметили точку M
; точки X
и Y
— центры вписанных окружностей треугольников ABM
и ACM
соответственно. Оказалось, что на прямой AM
существует точка Z
, для которой четырёхугольники BXZA
и CYZA
вписанные. Разложите вектор \overrightarrow{AM}
по векторам \overrightarrow{AB}
и \overrightarrow{AC}
.
Ответ. \overrightarrow{AM}=\frac{1}{2}\overrightarrow{AB}+\frac{1}{2}\overrightarrow{AC}
.
Решение. Рассмотрим случай, когда точка Z
лежит на отрезке AM
(см. рис.).
Четырёхугольник BXZA
вписанный, поэтому \angle XBA=\angle XZM
. Поскольку AX
— биссектриса вписанного угла BAM
, то BX=ZX
. Кроме того, MX
и BX
— биссектрисы углов AMB
и ABM
, поэтому
\angle ZMX=\angle AMX=\angle BMX,~\angle XZM=\angle XBA=\angle MBX.
Тогда \angle MXZ=\angle MXB
, значит, треугольники XBM
и XZM
равны по стороне и двум прилежащим к ней углам, поэтому BM=ZM
. Аналогично, треугольники YCM
и YZM
тоже равны, поэтому CM=ZM
. Значит, BM=CM
, поэтому AM
— медиана треугольника ABC
. Следовательно (см. задачу 4500),
\overrightarrow{AM}=\frac{1}{2}\overrightarrow{AB}+\frac{1}{2}\overrightarrow{AC}.
Аналогично для других случаев.
Источник: Журнал «Crux Mathematicorum». — 2018, № 4, задача 4238, с. 175
