13994. Окружность, вписанная в треугольник ABC
, касается его сторон BC
, CA
и AB
в точках D
, E
и F
соответственно. Точки M
и N
лежат на прямой EF
, причём MB\perp BC
и NC\perp BC
. Прямые DM
и DN
вторично пересекают вписанную окружность треугольника ABC
в точках P
и Q
соответственно, а прямые BQ
и CP
пересекаются в точке R
. Докажите, что прямая DR
проходит через середину отрезка MN
.
Решение. Пусть прямые DR
и MN
пересекаются в точке X
. Докажем, что X
— середина отрезка MN
.
Обозначим BC=a
, CA=b
, AB=c
, p
— полупериметр треугольника ABC
. Тогда (см. задачу 219)
AE=AF=p-a,~BD=BF=p-b,~CD=CE=p-c.
Если AB=AC
, утверждение очевидно. Пусть AC\gt AB
, и прямые прямые BC
и MN
пересекаются в точке T
(см. рис.). По теореме Менелая для треугольника ABC
и прямой MN
получаем
1=\frac{BT}{TC}\cdot\frac{CE}{EA}\cdot\frac{AF}{FB}=\frac{BT}{TC}\cdot\frac{p-c}{p-a}\cdot\frac{p-a}{p-b}=\frac{BT}{TC}\cdot\frac{p-c}{p-b},
откуда
\frac{BT}{TC}=\frac{p-b}{p-c}=\frac{BD}{CD}.
Прямоугольные треугольники TBM
и TCN
подобны, поэтому
\frac{BT}{TC}=\frac{MB}{NC}~\Rightarrow~\frac{MB}{NC}=\frac{BD}{CD}.
Тогда подобны прямоугольные треугольники MBD
и NCD
, значит,
\angle MDB=\angle NDC=\angle QDC,
поэтому по теореме об угле между касательной и хордой
\angle QPD=\angle QDC=\angle MDB=\angle PQD.
Следовательно, PD=DQ
и PQ\parallel BC
.
Обозначим
\angle QPD=\angle BDP=\angle CDQ=\angle PQD=\varphi.
Пусть прямые PQ
и DX
пересекаются в точке K
. Треугольник PRK
подобен треугольнику CRD
с коэффициентом \frac{KR}{RD}
, а треугольник QRK
— треугольнику BRD
с тем же коэффициентом \frac{KR}{RD}
. Значит,
\frac{PK}{KQ}=\frac{CD}{DB}=\frac{DN}{DM}.
Пусть p
и q
— расстояния от точки K
до боковых сторон соответственно DP
и DQ
равнобедренного треугольника PDQ
, а высоты треугольников DXM
и DXN
, проведённые из общей вершины X
, равны h_{1}
и h_{2}
соответственно. Тогда
p=PK\sin\varphi,~q=KQ\sin\varphi,~\frac{h_{1}}{p}=\frac{DX}{DK}=\frac{h_{2}}{q}.
Значит,
\frac{h_{1}}{h_{2}}=\frac{p}{q}=\frac{PK\sin\varphi}{KQ\sin\varphi}=\frac{PK}{KQ}=\frac{CD}{DB}=\frac{DN}{DM}~\Rightarrow~DM\cdot h_{1}=DN\cdot h_{2}.
Тогда
S_{\triangle DXM}=\frac{1}{2}DM\cdot h_{1}=\frac{1}{2}DN\cdot h_{2}=S_{\triangle DXN}.
Следовательно, DX
— медиана треугольника MDN
. Отсюда следует утверждение задачи.
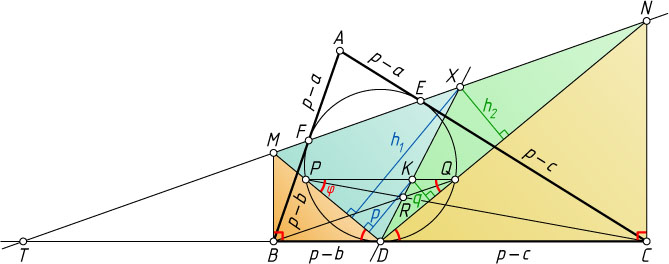
Источник: Журнал «Crux Mathematicorum». — 2018, № 8, задача 4277, с. 351
