1411. Высота прямоугольного треугольника, проведённая из вершины прямого угла, равна a
и образует угол \alpha
с медианой, проведённой из той же вершины. Найдите катеты треугольника.
Ответ. \frac{a\sqrt{2(1\pm\sin\alpha)}}{\cos\alpha}=\frac{a}{\sin\left(45^{\circ}\pm\frac{\alpha}{2}\right)}
.
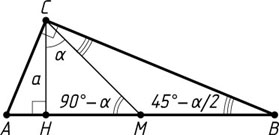
Решение. Первый способ. Пусть CH=a
— высота прямоугольного треугольника ABC
, проведённая из вершины C
прямого угла, CM
— медиана этого треугольника, причём \angle MCH=\alpha
.
Предположим, что BC\gt AC
. Тогда точка M
лежит между B
и H
. Из прямоугольного треугольника MCH
находим, что
MH=CH\tg\alpha=a\tg\alpha,~CM=\frac{CH}{\cos\alpha}=\frac{a}{\cos\alpha}.
Поскольку медиана прямоугольного треугольника, проведённая из вершины прямого угла, равна половине гипотенузы (см. задачу 1109), то
BM=AM=CM=\frac{a}{\cos\alpha},
BH=BM+MH=\frac{a}{\cos\alpha}+a\tg\alpha=\frac{a(1+\sin\alpha)}{\cos\alpha}.
Из прямоугольного треугольника BCH
по теореме Пифагора находим, что
BC=\sqrt{BH^{2}+CH^{2}}=\sqrt{\left(\frac{a(1+\sin\alpha)}{\cos\alpha}\right)^{2}+a^{2}}=
=\frac{a\sqrt{2(1+\sin\alpha)}}{\cos\alpha}.
Из прямоугольного треугольника ACH
аналогично находим, что
AC=\frac{a\sqrt{2(1-\sin\alpha)}}{\cos\alpha}.
Второй способ. Пусть CH=a
— высота прямоугольного треугольника ABC
, проведённая из вершины C
прямого угла, CM
— медиана этого треугольника, причём \angle MCH=\alpha
.
Предположим, что BC\gt AC
. Тогда точка M
лежит между B
и H
. Медиана прямоугольного треугольника, проведённая из вершины прямого угла, равна половине гипотенузы, поэтому BM=AM=CM
. Угол CMH
— внешний угол равнобедренного треугольника CMB
, значит,
\angle MBC=\frac{1}{2}\angle CMH=\frac{1}{2}(90^{\circ}-\alpha)=45^{\circ}-\frac{\alpha}{2}.
Следовательно,
BC=\frac{CH}{\sin\angle HBC}=\frac{a}{\sin\left(45^{\circ}-\frac{\alpha}{2}\right)}.
Аналогично находим, что
AC=\frac{CH}{\sin\angle HAC}=\frac{a}{\sin\left(45^{\circ}+\frac{\alpha}{2}\right)}.
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 1.9, с. 10
