14149. В основании треугольной пирамиды SABC
лежит прямоугольный треугольник ABC
с прямым углом C
. Основание высоты SO
этой пирамиды является серединой ребра AB
.
а) Докажите, что SA=SC
.
б) Найдите угол между плоскостями ASC
и ABC
, если AC=24
, AB=30
, SA=17
.
Ответ. \arctg\frac{8}{9}
.
Решение. а) Медиана, проведённая к гипотенузе прямоугольного треугольника, равна её половине (см. задачу 1109), значит, AO=OC
. Следовательно, прямоугольные треугольники ASO
и CSO
равны по двум катетам, а значит, их гипотенузы SA
и SC
также равны.
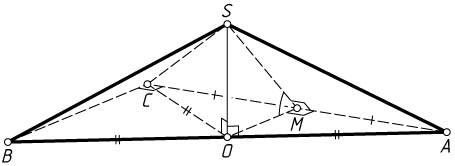
б) Пусть точка M
— середина стороны AC
. Поскольку треугольник SAC
равнобедренный, прямые AC
и SM
перпендикулярны. Прямая SO
перпендикулярна плоскости ABC
и лежащей в ней прямой AC
. По теореме о трёх перпендикулярах OM\perp AC
, поэтому угол SMO
искомый.
В прямоугольном треугольнике ASO
известно, что
SA=17,~AO=\frac{1}{2}AB=15,~SO=\sqrt{SA^{2}-AO^{2}}=8.
Отрезок MO
— средняя линия треугольника ABC
, значит,
MO=\frac{1}{2}BC=\frac{1}{2}\sqrt{AB^{2}-AC^{2}}=\sqrt{15^{2}-12^{2}}=9,\tg\angle SMO=\frac{SO}{MO}=\frac{8}{9}.
Следовательно, угол между плоскостями SAC
и ABC
равен \arctg\frac{8}{9}
.
Источник: ЕГЭ. — 2021
