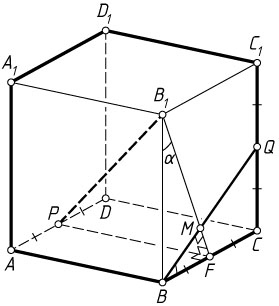
14169. Точки P
и Q
— середины рёбер соответственно AD
и CC_{1}
куба ABCDA_{1}B_{1}C_{1}D_{1}
.
а) Докажите, что прямая BQ
перпендикулярна прямой B_{1}P
.
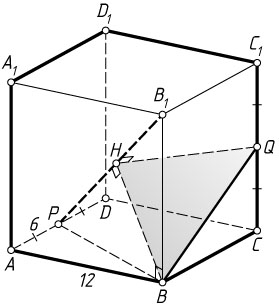
б) Пусть H
— проекция точки Q
на прямую B_{1}P
. Найдите PH
, если AB=12
.
Ответ. 10.
Решение. а) Пусть F
— середина ребра BC
. Тогда PF
— перпендикуляр к плоскости BCC_{1}
, а B_{1}F
— ортогональная проекция наклонной PB_{1}
на эту плоскость.
Рассмотрим квадрат BCC_{1}B_{1}
. Пусть M
— точка пересечения отрезков B_{1}F
и BQ
, а \angle BB_{1}F=\angle CBQ=\alpha
(углы равны, так как равны прямоугольные треугольники BB_{1}F
и CBQ
). Тогда
\angle BMF=180^{\circ}-\angle FBM-\angle BFM=180^{\circ}-\alpha-(90^{\circ}-\alpha)=90^{\circ},
т. е. B_{1}F\perp BQ
. Следовательно, по теореме о трёх перпендикулярах B_{1}P\perp BQ
.
б) Поскольку прямая BQ
перпендикулярна прямой B_{1}P
, то плоскость, проходящая через прямую BQ
и общий перпендикуляр скрещивающихся прямых BQ
и PB_{1}
, перпендикулярна прямой PB_{1}
. Эта плоскость пересекает прямую PB_{1}
в точке, которая является ортогональной проекцией каждой точки прямой BQ
на прямую PB_{1}
, т. е. в точке H
.
Из прямоугольного треугольника BB_{1}P
получаем
HP=\frac{PB^{2}}{PB_{1}}=\frac{6^{2}+12^{2}}{18}=10
(см. задачу 2728).
Источник: Диагностические и тренировочные задачи ЕГЭ. — 2020

