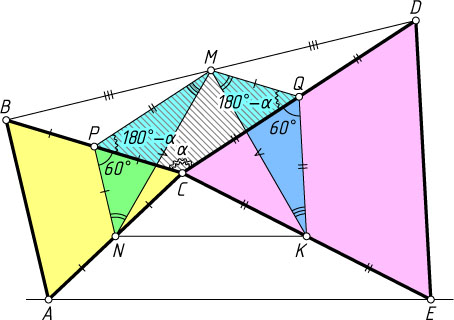
1423. Два равносторонних треугольника ABC
и CDE
расположены по одну сторону от прямой AE
и имеют единственную общую точку C
. Пусть M
, N
и K
— середины отрезков BD
, AC
и CE
соответственно. Докажите, что треугольник MNK
— равносторонний.
Указание. Пусть P
и Q
— середины отрезков BC
и DC
соответственно. Докажите, что треугольники MPN
и KQM
равны.
Решение. Пусть P
и Q
— середины отрезков BC
и DC
соответственно. Докажем, что треугольники MPN
и KQM
равны. В самом деле (см. задачу 1109),
PN=PC=MQ,~PM=CQ=QK,
\angle MPN=\angle MPC+\angle CPN=\angle MQC+60^{\circ}=\angle MQC+\angle CQK=\angle KQM.
Следовательно, MN=MK
.
Осталось доказать, что \angle NMK=60^{\circ}
. Пусть \angle BCD=\alpha
. Поскольку каждый из углов MNC
и MKC
меньше 60^{\circ}
, то
\angle NMK=\angle PMQ-\angle PMN-\angle QMK=\alpha-\angle PMN-\angle PNM=
=\alpha-180^{\circ}+\angle NPM=\alpha-180^{\circ}+\angle NPC+\angle CPM=
=\alpha-180^{\circ}+60^{\circ}+(180^{\circ}-\alpha)=60^{\circ}.