1437. В ромбе ABCD
точка Q
делит сторону BC
в отношении 1:3
, считая от вершины B
, а точка E
— середина стороны AB
. Известно, что медиана CF
треугольника CEQ
равна 2\sqrt{2}
, а EQ=\sqrt{2}
. Найдите радиус окружности, вписанной в ромб ABCD
.
Ответ. \frac{\sqrt{7}}{2}
.
Указание. Воспользуйтесь формулой для медианы треугольника (см. задачу 4014):
m^{2}=\frac{1}{4}(2a^{2}+2b^{2}-c^{2}),
где a
, b
, c
— стороны треугольника, m
— медиана, проведённая к стороне, равной c
.
Решение. Воспользуемся формулой для медианы треугольника (см. задачу 4014):
m^{2}=\frac{1}{4}(2a^{2}+2b^{2}-c^{2}),
где a
, b
, c
— стороны треугольника, m
— медиана, проведённая к стороне, равной c
.
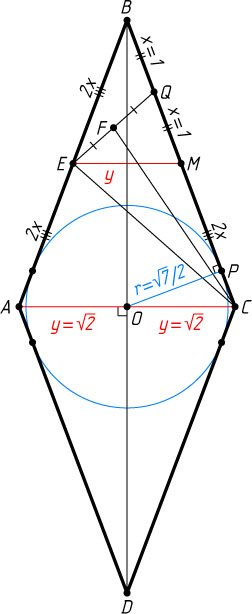
Обозначим BQ=x
, AC=2y
. Пусть O
— точка пересечения диагоналей ромба ABCD
, M
— середина стороны BC
. Тогда
OC=y,~AB=BC=4x,~MQ=x,
а так как ME
— средняя линия треугольника ABC
, то ME=\frac{1}{2}AC=y
.
Поскольку EQ
— медиана треугольника BEM
, то
EQ^{2}=\frac{1}{4}(2BE^{2}+2EM^{2}-BM^{2}),~\mbox{или}~2=\frac{1}{4}(2\cdot4x^{2}+2y^{2}-4x^{2}),
или
2x^{2}+y^{2}=4.
Поскольку CE
— медиана треугольника ABC
, то
CE^{2}=\frac{1}{4}(2AC^{2}+2BC^{2}-AB^{2})=\frac{1}{4}(8y^{2}+32x^{2}-16x^{2})=4x^{2}+2y^{2}.
Поскольку CF
— медиана треугольника CEQ
, то
8=CF^{2}=\frac{1}{4}(2CE^{2}+2CQ^{2}-EQ^{2})=\frac{1}{4}(8x^{2}+4y^{2}+18x^{2}-2)=\frac{1}{4}(26x^{2}+4y^{2}-2),
откуда
13x^{2}+y^{2}=17.
Из полученной системы уравнений
\syst{2x^{2}+y^{2}=4\\13x^{2}+y^{2}=17\\}
находим, что x=1
, y=\sqrt{2}
. Тогда
OB^{2}=BC^{2}-OC^{2}=16-2=14.
Пусть OP
— высота прямоугольного треугольника BOC
. Тогда OP
— радиус окружности, вписанной в ромб. Поскольку BC\cdot OP=OB\cdot OC
, то
OP=\frac{OB\cdot OC}{BC}=\frac{\sqrt{14}\cdot\sqrt{2}}{4}=\frac{\sqrt{7}}{2}.
Источник: Вступительный экзамен на факультет вычислительной математики и кибернетики (ВМК) МГУ. — 1993, № 4, вариант 2
Источник: Журнал «Математика в школе». — 1994, № 1, с. 46
