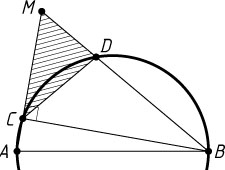
1440. Точка M
, лежащая вне круга с диаметром AB
, соединена с точками A
и B
. Отрезки MA
и MB
пересекают окружность в точках C
и D
соответственно. Площадь круга, вписанного в треугольник AMB
, в четыре раза больше, чем площадь круга, вписанного в треугольник CMD
. Найдите углы треугольника AMB
, если известно, что один из них в два раза больше другого.
Ответ. 60^{\circ}
, 40^{\circ}
, 80^{\circ}
.
Указание. Треугольник MCD
подобен треугольнику MBA
с коэффициентом \frac{1}{2}
.
Решение. Поскольку
\angle MCD=180^{\circ}-\angle ACD=\angle ABD,
то треугольник MCD
подобен треугольнику MBA
по двум углам. Площадь круга, вписанного в треугольник MCD
, в четыре раза меньше площади круга, вписанного в треугольник MBA
, поэтому радиус первого круга вдвое меньше радиуса второго. Следовательно, коэффициент подобия треугольников MCD
и MBA
равен \frac{1}{2}
. Значит (см. задачу 19),
\cos\angle CMB=\frac{MC}{MB}=\frac{1}{2},
а так как угол CMB
— острый (точка M
расположена вне данного круга), то
\angle AMB=\angle CMB=60^{\circ}.
Угол при вершине M
треугольника AMB
не может быть вдвое меньше угла A
или B
, так как в противном случае один из углов A
или B
равен 120^{\circ}\gt90^{\circ}
, что невозможно. Если же угол M
вдвое больше угла A
, то угол B
равен 90^{\circ}
, что также невозможно (в этом случае прямая MB
касается данной окружности). Аналогично докажем, что угол M
не может быть вдвое меньше угла B
.
Таким образом, либо угол A
вдвое больше угла B
, либо наоборот. В каждом из этих случаев один из углов равен 40^{\circ}
, а второй 80^{\circ}
.
Источник: Вступительный экзамен на геологический факультет МГУ. — 1993, вариант 2, № 5
Источник: Нестеренко Ю. В., Олехник С. Н., Потапов М. К. Задачи вступительных экзаменов по математике. — М.: Факториал, 1995. — с. 612
Источник: Журнал «Математика в школе». — № 1, 1994, с. 51
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 15.3, с. 122
