1459. Известно, что в четырёхугольник можно вписать и около него можно описать окружность. Докажите, что отрезки, соединяющие точки касания противоположных сторон с вписанной окружностью, взаимно перпендикулярны.
Указание. Примените теорему об угле между пересекающимися хордами.
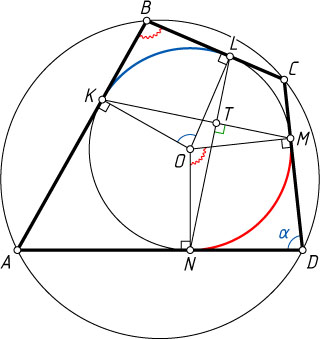
Решение. Пусть ABCD
— данный четырёхугольник; K
, L
, M
и N
— точки касания его сторон соответственно AB
, BC
, CD
и AD
с вписанной окружностью; T
— точка пересечения отрезков KM
и NL
; O
— центр вписанной окружности четырёхугольника ABCD
. Обозначим \angle ADC=\alpha
. Тогда
\angle MON=180^{\circ}-\alpha=\angle ABC,~\angle KOL=180^{\circ}-\angle ABC=180^{\circ}-(180^{\circ}-\alpha)=\alpha.
Следовательно,
\angle MTN=\frac{\cup MN+\cup KL}{2}=\frac{\angle MON+\angle KOL}{2}=\frac{180^{\circ}}{2}=90^{\circ}
(см. задачу 26).
Источник: Пржевальский Е. Собрание геометрических теорем и задач. — М.: Типография Г. Лисснера и Д. Собко, 1909. — № 156, с. 45
Источник: Понарин Я. П. Элементарная геометрия. — Т. 1: Планиметрия, преобразования плоскости. — М.: МЦНМО, 2004. — № 7.20, с. 59
Источник: Мерзляк А. Г., Поляков В. М. Геометрия. 8 класс. Углублённый уровень. — М.: Вентана-Граф, 2019. — № 2.40, с. 19
