14660. Сечение (не обязательно прямоугольного) параллелепипеда ABCDA_{1}B_{1}C_{1}D_{1}
плоскостью представляет из себя пятиугольник с вершинами на рёбрах AA_{1}
, BB_{1}
, CC_{1}
, CD
и DA
. Его стороны в порядке обхода, начиная с одной из вершин, равны 2, 3, 4, 5, 7. Найдите угол между сторонами длины 5 и 7.
Ответ. 60^{\circ}
.
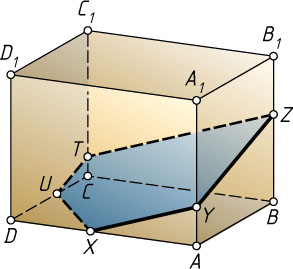
Решение. Стороны сечения, лежащие на противоположных гранях параллелепипеда, параллельны. Таким образом, сечение представляет собой пятиугольник XYZTU
(см. рис.), в котором XY\parallel ZT
, YZ\parallel TU
(см. задачу 8009).
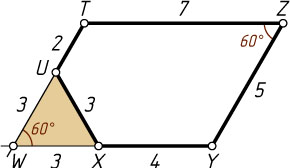
Продолжим стороны XY
и TU
до пересечения в точке W
. Получим параллелограмм WYZT
. Тогда
XY\lt YW=ZT,~TU\lt TW=YZ.
Значит, две наибольшие стороны могут быть только соседними сторонами YZ
и ZT
. Не умаляя общности, считаем, что
YZ=5,~ZT=7,~TU=2,~UX=3,~XY=4.
Тогда
WX=7-4=3,~WU=5-2=3,
т. е. треугольник WXU
равносторонний. Следовательно, угол YZT
нашего параллелограмма равен 60^{\circ}
.
Автор: Берлов С. Л.
Источник: Санкт-Петербургская (Ленинградская) математическая олимпиада. — 2021, первый тур, задача 3, 10 класс

