1469. Четырёхугольник ABCD
вписан в окружность, DC=m
, DA=n
. На стороне BA
взяты точки A_{1}
и K
, а на стороне BC
— точки C_{1}
и M
. Известно, что BA_{1}=a
, BC_{1}=c
, BK=BM
и что отрезки A_{1}M
и C_{1}K
пересекаются на диагонали BD
. Найдите BK
и BM
.
Ответ. \frac{ac(n-m)}{an-cm}
.
Решение. Рассмотрим случай, когда точка A_{1}
расположена между точками B
и K
, а точка C_{1}
— между точками B
и M
. Пусть P
— точка пересечения отрезков KM
и BD
,
\angle ADC=2\alpha,~BK=BM=x.
По свойству вписанного четырёхугольника
\angle ABC=180^{\circ}-\angle ADC=180^{\circ}-2\alpha.
Тогда
\angle BKM=\angle BMK=\frac{1}{2}(180^{\circ}-\angle ABC)=\frac{1}{2}(180^{\circ}-(180^{\circ}-2\alpha))=\alpha.
Проведём биссектрису DQ
треугольника ADC
. Тогда
\angle ADQ=\angle BMP=\alpha,~\angle QAD=\angle CAD=\angle CBD=\angle CBP,
поэтому треугольники ADQ
и BMP
подобны. Значит, \frac{AD}{BM}=\frac{DQ}{PM}
. Аналогично докажем, что \frac{CD}{KB}=\frac{DQ}{PK}
. Из этих равенств следует, что
\frac{PK}{PM}=\frac{AD}{CD}=\frac{n}{m}.
Поскольку отрезки KC_{1}
, MA_{1}
и BP
пересекаются в одной точке, то по теореме Чевы (см. задачу 1621)
\frac{BA_{1}}{A_{1}K}\cdot\frac{KP}{PM}\cdot\frac{MC_{1}}{C_{1}B}=1,
или
\frac{a}{x-a}\cdot\frac{n}{m}\cdot\frac{x-c}{c}=1.
Из этого уравнения находим, что x=\frac{ac(n-m)}{an-cm}
. Для остальных случаев аналогично.
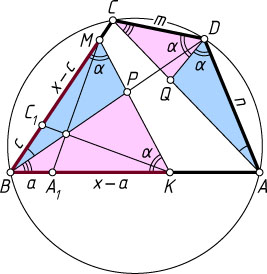
Автор: Шарыгин И. Ф.
Источник: Соросовская олимпиада. — 1994, I, III тур, 1-й раунд, 11 класс
