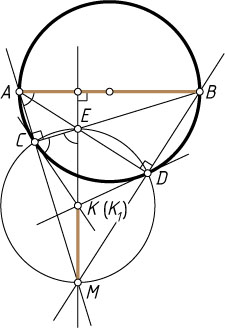
1471. На окружности с диаметром AB
взяты точки C
и D
. Прямые AC
и BD
пересекаются в точке M
. Касательные к окружности в точках C
и D
пересекаются в точке K
. Докажите, что прямая MK
перпендикулярна AB
.
Решение. Точки C
и D
лежат на окружности с диаметром AB
, поэтому \angle ACB=\angle ADB=90^{\circ}
. Значит, AD
и BC
— высоты треугольника AMB
. Пусть E
— точка их пересечения. Поскольку высоты треугольника пересекаются в одной точке, ME\perp AB
.
Предположим, что точки C
и D
расположены по одну сторону от прямой AB
, а точка M
лежит вне окружности.
Из точек C
и D
отрезок ME
виден под прямым углом, значит, эти точки лежат на окружности с диаметром ME
. Пусть K_{1}
— центр этой окружности. Тогда
\angle BCK_{1}=\angle ECK_{1}=\angle CEK_{1}=\angle CEM=\angle MAB=\angle CAB=\frac{1}{2}\smile BDC.
По теореме, обратной теореме об угле между касательной и хордой (см. задачу 144), CK_{1}
— касательная к окружности с диаметром AB
. Аналогично DK_{1}
— также касательная к этой окружности. Следовательно, точка K_{1}
совпадает с точкой K
, а так как точка K_{1}
лежит на прямой, перпендикулярной AB
, то MK\perp AB
.
Аналогично для остальных случаев.
Источник: Шарыгин И. Ф. Геометрия: 9—11 кл.: От учебной задачи к творческой: Учебное пособие. — М.: Дрофа, 1996. — № 919, с. 113
Источник: Кушнир И. А. Геометрия. Поиск и вдохновение. — М.: МЦНМО, 2013. — задача 15, с. 276
