1472. В прямоугольную трапецию вписана окружность радиуса r
. Меньшее основание трапеции равно a
. Найдите расстояние от точки пересечения диагоналей трапеции до центра окружности.
Ответ. \frac{r(2r-a)}{a}
.
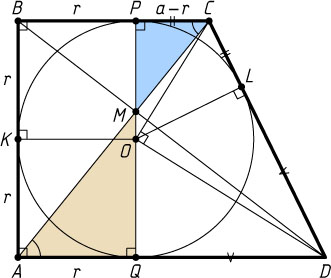
Решение. Пусть окружность с центром O
касается меньшего основания BC=a
трапеции ABCD
в точке P
, большего основания AD
— в точке Q
, меньшей боковой стороны AB
— в точке K
, большей боковой стороны CD
— в точке L
. Докажем сначала, что M
— точка пересечения диагоналей трапеции лежит на отрезке PQ
. Для этого достаточно доказать, что \angle PMC=\angle QMA
.
Действительно, поскольку OPBK
— квадрат, а OL=r
— высота прямоугольного треугольника COD
, проведённая из вершины прямого угла, то
BP=OK=r,~CL=CP=BC-BP=a-r,~DQ=DL=\frac{OL^{2}}{CL}=\frac{r^{2}}{a-r}
(см. задачу 314),
AD=AQ+DQ=r+\frac{r^{2}}{a-r}=\frac{ar}{a-r}.
Треугольники PMC
и QMA
подобны, так как
\angle PCM=\angle MAQ,~\frac{PC}{AQ}=\frac{a-r}{r},~\frac{CM}{AM}=\frac{BC}{AD}=\frac{a}{\frac{ar}{a-r}}=\frac{a-r}{r}=\frac{PC}{AQ}.
Следовательно, \angle PMC=\angle QMA
, что и требовалось доказать.
Из подобия треугольников PMC
и QMA
также следует, что \frac{PM}{QM}=\frac{CP}{AQ}=\frac{a-r}{r}
, поэтому
PM=PQ\cdot\frac{PM}{PQ}=2r\cdot\frac{a-r}{a-r+r}=\frac{2r(a-r)}{a}.
Следовательно,
OM=OP-PM=r-\frac{2r(a-r)}{a}=\frac{r(2r-a)}{a}.
Источник: Шарыгин И. Ф. Геометрия: 9—11 кл.: От учебной задачи к творческой: Учебное пособие. — М.: Дрофа, 1996. — № 713, с. 90
