1488. В четырёхугольнике ABCD
углы A
и C
равны 90^{\circ}
. Докажите, что периметр вписанного в ABCD
четырёхугольника не меньше, чем 2AC
.
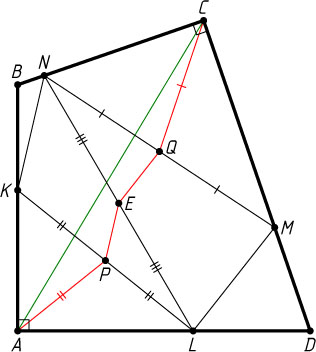
Решение. Пусть вершины K
, N
, M
и L
четырёхугольника KNML
лежат на сторонах соответственно AB
, BC
, CD
и AD
четырёхугольника ABCD
, а точки P
, E
и Q
— середины отрезков KL
, LN
и MN
соответственно. Тогда AP
и QC
— медианы прямоугольных треугольников AKL
и CMN
, проведённые из вершин прямых углов, а PE
и QE
— средние линии треугольников KLN
и MLN
. Значит (см. задачу 1109),
AP=\frac{1}{2}LK,~PE=\frac{1}{2}KN,~EQ=\frac{1}{2}ML,~QC=\frac{1}{2}MN,
поэтому
LK+KN+ML+MN=2AP+2PE+2QE+2CQ=2(AP+PE+EQ+QC)\geqslant2AC.
Что и требовалось доказать.
Источник: Шарыгин И. Ф. Геометрия: 9—11 кл.: От учебной задачи к творческой: Учебное пособие. — М.: Дрофа, 1996. — № 1038, с. 128
