1530. Дан треугольник ABC
. На продолжении стороны AC
за точку C
взята точка N
, причём AC=2CN
. Точка M
находится на стороне BC
, причём BM:MC=1:3
. В каком отношении прямая MN
делит сторону AB
?
Ответ. 1:9
, считая от точки B
.
Указание. Проведите через вершину B
прямую, параллельную стороне AC
, и рассмотрите две пары подобных треугольников (или примените теорему Менелая, см. задачу 1622).
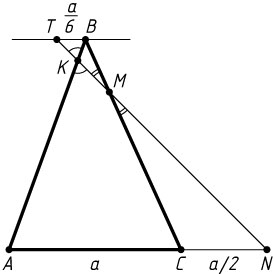
Решение. Первый способ. Через точку B
проведём прямую, параллельную AC
. Пусть прямая MN
пересекает её в точке T
, а прямую AB
— в точке K
.
Обозначим AC=a
. Тогда CN=\frac{1}{2}a
, AN=\frac{3}{2}a
. Из подобия треугольников TBM
и NCM
(коэффициент \frac{1}{3}
) находим, что
TB=\frac{1}{3}CN=\frac{1}{6}a,
а из подобия треугольников TBK
и NAK
—
\frac{BK}{AK}=\frac{BT}{AN}=\frac{\frac{1}{6}a}{\frac{3}{2}a}=\frac{1}{9}.
Второй способ. Через точку C
проведём прямую, параллельную MN
. Пусть эта прямая и прямая MN
пересекают сторону AB
в точках P
и K
соответственно. Положим AP=6t
. Тогда по теореме о пропорциональных отрезках \frac{KP}{AP}=\frac{CN}{AC}=\frac{1}{2}
, поэтому KP=\frac{1}{2}AP=3t
, а так как \frac{BK}{KP}=\frac{BM}{MC}=\frac{1}{3}
, то BK=\frac{1}{3}KP=t
. Следовательно,
\frac{BK}{KA}=\frac{BK}{BK+KP+AP}=\frac{t}{t+3t+6t}=\frac{1}{9}.
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — с. 42
