1534. Точки A_{1}
и C_{1}
расположены на сторонах BC
и AB
треугольника ABC
. Отрезки AA_{1}
и CC_{1}
пересекаются в точке M
. В каком отношении прямая BM
делит сторону AC
, если AC_{1}:C_{1}B=2:3
и BA_{1}:A_{1}C=1:2
?
Ответ. 1:3
, считая от точки A
.
Указание. Через вершину B
проведите прямую, параллельную AC
, или примените теорему Чевы (см. задачу 1621).
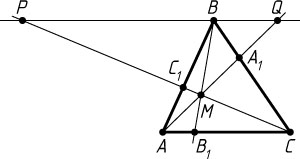
Решение. Через вершину B
проведём прямую, параллельную AC
, и продолжим CC_{1}
и AA_{1}
до пересечения с ней в точках P
и Q
соответственно. Если B_{1}
— точка пересечения прямой BM
со стороной AC
, то треугольник PBM
подобен треугольнику CB_{1}M
, а треугольник QMB
— треугольнику AB_{1}M
, причём коэффициент подобия один и тот же — \frac{BM}{MB_{1}}
. Поэтому
\frac{AB_{1}}{B_{1}C}=\frac{BQ}{BP}=\frac{\frac{1}{2}AC}{\frac{3}{2}AC}=\frac{1}{3}.
(BQ=\frac{1}{2}AC
из подобия треугольников BA_{1}Q
и CA_{1}A
, а BP=\frac{3}{2}AC
из подобия треугольников PBC_{1}
и CAC_{1}
).
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 6.9, с. 46
