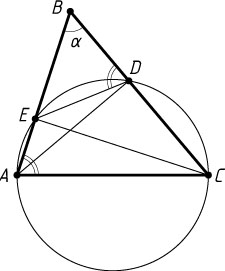
1595. В треугольнике ABC
проведены высоты AD
и CE
. Найдите AC
, если BC=a
, AB=b
, \frac{DE}{AC}=k
.
Ответ. \sqrt{a^{2}+b^{2}\pm2abk}
.
Указание. Треугольники EDB
и CBA
подобны (см. задачу 19). Рассмотрите два случая: \angle B\lt90^{\circ}
и \angle B\gt90^{\circ}
.
Решение. Обозначим \angle ABC=\alpha
. Если \alpha\lt90^{\circ}
, то треугольники EDB
и CAB
подобны с коэффициентом \cos\alpha
(см. задачу 19), т. е. \cos\alpha=\frac{DE}{AC}=k
. Тогда по теореме косинусов
AC^{2}=BA^{2}+BC^{2}-2BA\cdot BC\cdot\cos\alpha=b^{2}+a^{2}-2abk.
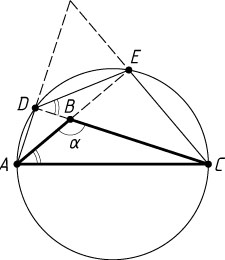
Если \alpha\gt90^{\circ}
, то треугольники EDB
и CBA
подобны с коэффициентом (-\cos\alpha)
, т. е. -\cos\alpha=\frac{DE}{AC}=k
. Тогда
AC^{2}=a^{2}+b^{2}+2abk.
