16000. На отрезке AB
взята точка C
, и на отрезках AB
, BC
, CA
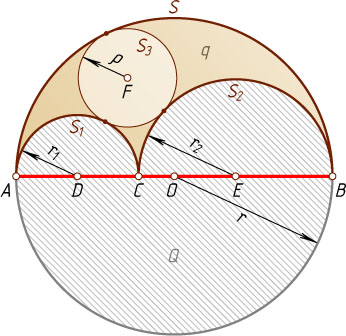
как на диаметрах построены по одну сторону от AB
полуокружности S
, S_{1}
, S_{2}
с центрами O
, D
, E
и радиусами r
, r_{1}
, r_{2}
соответственно. Окружность S_{3}
с центром F
и радиусом \rho
касается всех трёх полуокружностей. Докажите, что
\frac{\rho}{r}=\frac{r^{2}-r_{1}^{2}-r_{2}^{2}}{r^{2}+r_{1}^{2}+r_{2}^{2}}=\frac{q}{Q},
где q
— площадь криволинейного треугольника ACB
(арбелоса Архимеда), а Q
— площадь заштрихованной фигуры, образованной полуокружностями S_{1}
, S_{2}
и лежащей по другую сторону от AB
полуокружностью окружности S
.
Решение. Поскольку
\rho=\frac{2rr_{1}r_{2}}{r^{2}+r_{1}^{2}+r_{2}^{2}}
(см. задачу 4867) и
q=\frac{1}{2}\pi r^{2}-\frac{1}{2}\pi r_{1}^{2}-\frac{1}{2}\pi r_{2}^{2}=\frac{1}{2}\pi(r^{2}-r_{1}^{2}-r_{2}^{2}),
Q=\frac{1}{2}\pi r^{2}+\frac{1}{2}\pi r_{1}^{2}+\frac{1}{2}\pi r_{2}^{2}=\frac{1}{2}\pi(r^{2}+r_{1}^{2}+r_{2}^{2}),
то
\frac{\rho}{r}=\frac{\frac{2rr_{1}r_{2}}{r^{2}+r_{1}^{2}+r_{2}^{2}}}{r}=\frac{2r_{1}r_{2}}{r^{2}+r_{1}^{2}+r_{2}^{2}}
и
\frac{q}{Q}=\frac{\frac{1}{2}\pi(r^{2}-r_{1}^{2}-r_{2}^{2})}{\frac{1}{2}\pi(r^{2}+r_{1}^{2}+r_{2}^{2})}=\frac{r^{2}-r_{1}^{2}-r_{2}^{2}}{r^{2}+r_{1}^{2}+r_{2}^{2}}.
Значит,
\frac{\rho}{r}=\frac{q}{Q}~\Leftrightarrow~\frac{2r_{1}r_{2}}{r^{2}+r_{1}^{2}+r_{2}^{2}}=\frac{r^{2}-r_{1}^{2}-r_{2}^{2}}{r^{2}+r_{1}^{2}+r_{2}^{2}}~\Leftrightarrow
\Leftrightarrow~2r_{1}r_{2}=r^{2}-r_{1}^{2}-r_{2}^{2}~\Leftrightarrow~(r_{1}+r_{2})^{2}=r^{2}.
Последнее неравенство верно, так как r_{1}+r_{2}=r
. Отсюда следует утверждение задачи.
Источник: Журнал «Crux Mathematicorum». — 1977, № 8, с. 217
