16047. Произвольная точка P
лежит на описанной окружности \Gamma
данного треугольника ABC
и отлична от его вершин. Окружности \Gamma_{1}
и \Gamma_{2}
проходят через точку P
, причём \Gamma_{1}
касается прямой AB
в точке B
, а \Gamma_{2}
касается прямой AC
в точке C
. Окружности \Gamma_{1}
и \Gamma_{2}
пересекаются в точках P
и Q
. Докажите, что:
а) точка Q
лежит на прямой BC
;
б) все прямые PQ
проходят через фиксированную точку окружности \Gamma
.
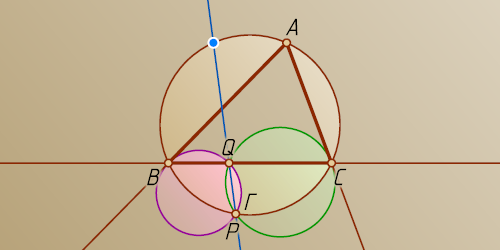
Решение. Рассмотрим случай, изображённый на рисунке.
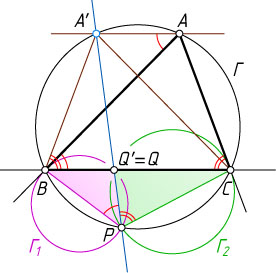
Через вершину A
проведём прямую, параллельную стороне BC
. Пусть эта прямая вторично пересекает окружность в точке A'
. Докажем, что все прямые PQ
проходят через точку A'
.
Действительно, пусть прямая A'P
пересекает сторону BC
в точке Q'
. Тогда
\angle BPQ'=\angle BPA'=\angle BAA'=\angle ABC=\angle ABQ',
поэтому прямая AB
— касательная к описанной окружности треугольника BPQ'
(см задачу 144). В то же время,
\angle CPQ'=\angle CPA'=\angle CBA'=\angle BCA=\angle ACQ',
поэтому прямая AC
— касательная к описанной окружности треугольника CPQ'
.
Таким образом, точка Q'
, лежащая на прямой BC
, — отличная от P
точка пересечения окружностей, проходящих через точку P
и касающихся прямых AB
и AC
точках B
и C
соответственно. Значит, Q'
совпадает с Q
. Отсюда следуют оба утверждения задачи.
С некоторыми изменениями приведённые рассуждения годятся для любого другого случая.
Источник: Журнал «Crux Mathematicorum». — 1990, № 6, задача 1436 (1989, с. 110), с. 186

