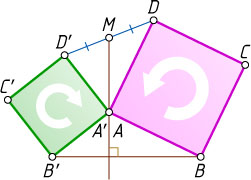
16115. Даны противоположно ориентированные квадраты ABCD
и A'B'C'D'
с совпадающими вершинами A
и A'
(см. рис.). Точка M
— середина отрезка DD'
. Докажите, что AM\perp BB'
и BB'=2AM
.
Решение. Рассмотрим поворот на 90^{\circ}
вокруг точки A
, переводящий точку B'
в D'
, а точку D
в B
. Тогда
\overrightarrow{AB'}\cdot\overrightarrow{AD}=\overrightarrow{AD'}\cdot\overrightarrow{AB},
а так как
\overrightarrow{AM}=\frac{1}{2}(\overrightarrow{AD}+\overrightarrow{AD'})
(см. задачу 4500), то
2\overrightarrow{AM}\cdot\overrightarrow{BB'}=(\overrightarrow{AD}+\overrightarrow{AD'})(\overrightarrow{AB'}-\overrightarrow{AB})=
=\overrightarrow{AD}\cdot\overrightarrow{AB'}-\overrightarrow{AD}\cdot\overrightarrow{AB}+\overrightarrow{AD'}\cdot\overrightarrow{AB'}-\overrightarrow{AD'}\cdot\overrightarrow{AB}=
=\overrightarrow{AD}\cdot\overrightarrow{AB'}-0+0-\overrightarrow{AD'}\cdot\overrightarrow{AB}=0.
Следовательно, AM\perp BB'
.
Поскольку
|\overrightarrow{AB'}|=|\overrightarrow{AD'}|,~|\overrightarrow{AB}|=|\overrightarrow{AD}|~\mbox{и}~\angle BAB'+\angle DAD'=180^{\circ},
то
\overrightarrow{AB}\cdot\overrightarrow{AB'}=-\overrightarrow{AD}\cdot\overrightarrow{AD'}.
Значит,
4|\overrightarrow{AM}|^{2}=2|\overrightarrow{AM}|\cdot2|\overrightarrow{AM}|=(\overrightarrow{AD}+\overrightarrow{AD'})^{2}=|\overrightarrow{AD}|^{2}+2\overrightarrow{AD}\cdot\overrightarrow{AD'}+|\overrightarrow{AD'}|^{2}=
=|\overrightarrow{AB}|^{2}-2\overrightarrow{AB}\cdot\overrightarrow{AB'}+|\overrightarrow{AB'}|^{2}=(\overrightarrow{AB}-\overrightarrow{AB'})^{2}=|\overrightarrow{BB'}|^{2}.
Следовательно, 2AM=BB'
.
Источник: Журнал «Crux Mathematicorum». — 1997, № 4, задача A188, с. 240
