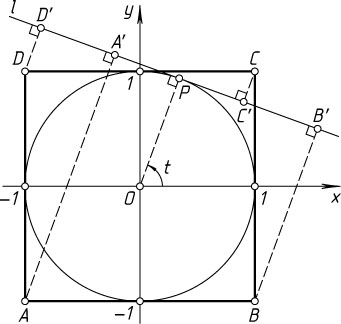
16126. Из вершин A
, B
, C
и D
квадрата ABCD
опустили перпендикуляры AA'
, BB'
, CC'
и DD'
на касательную l
к вписанной в квадрат окружности. Докажите, что AA'\cdot CC'=BB'\cdot DD'
.
Решение. Пусть O
— центр окружности, а её радиус равен 1. Введём систему координат, как показано на рисунке. Тогда координаты точек A
, B
, C
и D
— (-1;-1)
, (1;-1)
, (1;1)
, (-1;1)
соответственно.
Пусть P(\cos t;\sin t)
— точка касания. Тогда уравнения окружности и прямой имеют вид
x^{2}+y^{2}=1~\mbox{и}~x\cos t+y\sin t-1=0.
По формуле расстояния от точки до прямой (см. задачу 4249) получаем
AA'=|-\cos t-\sin t-1|,~BB'=|\cos t-\sin t-1|,
CC'=|\cos t+\sin t-1|,~DD'=|-\cos t+\sin t-1|.
Тогда
AA'\cdot CC'=|(\cos t+\sin t+1)(\cos t+\sin t-1)|\cdot|(\cos t+\sin t)^{2}-1|=|\sin2t|,
BB'\cdot DD'=|(\cos t-\sin t-1)(\cos t-\sin t+1)|\cdot|(\cos t-\sin t)^{2}-1|=|\sin2t|.
Следовательно,
AA'\cdot CC'=BB'\cdot DD'.
Что и требовалось доказать.
Источник: Журнал «Crux Mathematicorum». — 1998, № 4, задача 2237 (1997, с. 169), с. 251
