16128. На сторонах AB
и AC
вне треугольника ABC
построены треугольники AXB
и AYC
. При этом углы XAB
и YAC
фиксированы, а \angle XBA+\angle YCA=180^{\circ}
. Докажите, что все прямые XY
проходят через одну точку.
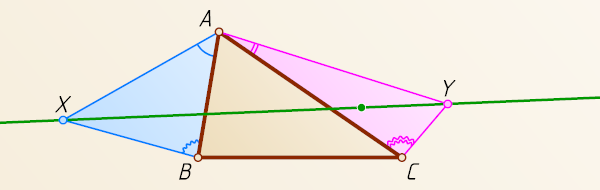
Решение. Рассмотрим случай, изображённый на рисунке.
Пусть \Gamma
— описанная окружность треугольника ABC
. Тогда точка Z
пересечения прямых BX
и CY
лежит на этой окружности, так как
\angle ABZ=180^{\circ}-\angle XBA=\angle YCA=180^{\circ}-\angle ACZ,
т. е. четырёхугольник ABZC
вписан в окружность \Gamma
.
Пусть прямые AX
и AY
вторично пересекают окружность \Gamma
в точках D
и E
соответственно. Поскольку прямые AX
и AY
фиксированы, точки D
и E
тоже фиксированы. Пусть P
— точка пересечения прямых BE
и CD
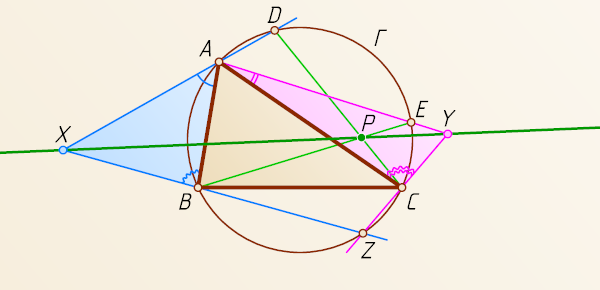
. Шестиугольник ADCZBE
(самопересекающийся) вписан в окружность \Gamma
, поэтому по теореме Паскаля точки пересечения прямых, содержащих его противоположные стороны, лежат на одной прямой (см. примечание к задаче 6390). Следовательно, каждая прямая XY
проходит через точку P
. Отсюда получаем утверждение задачи.
Источник: Журнал «Crux Mathematicorum». — 1998, № 7, задача 2265 (1997, с. 364), с. 433

