6390. Теорема Паскаля. Докажите, что во всяком вписанном шестиугольнике точки пересечения прямых, содержащих противоположные стороны (если эти стороны не параллельны), лежат на одной прямой.
Указание. Примените теорему Менелая и теорему о равенстве произведений всей секущей на её внешнюю часть.
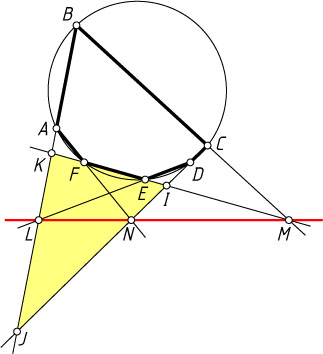
Решение. Рассмотрим случай, изображённый на рис. 1. Пусть ABCDEF
— вписанный шестиугольник, прямые AB
и DE
пересекаются в точке L
, прямые BC
и EF
— в точке M
, прямые CD
и AF
— в точке N
. Требуется доказать, что точки L
, M
и N
лежат на одной прямой.
Пусть прямые CD
и EF
пересекаются в точке I
, прямые AB
и CD
— в точке J
, прямые AB
и EF
— в точке K
. Из теоремы Менелая (см. задачу 1622), применённой к треугольнику IJK
, следует, что точки L
, M
и N
лежат на одной прямой, если \frac{LJ}{LK}\cdot\frac{MK}{MI}\cdot\frac{IN}{NJ}=1
.
Докажем это равенство. Применяя теорему Менелая к треугольнику IJK
и прямым DE
, BC
и AF
, получим, что
\frac{ID}{DJ}\cdot\frac{JL}{LK}\cdot\frac{KE}{EI}=1,~\frac{JB}{BK}\cdot\frac{KM}{MI}\cdot\frac{IC}{CJ}=1,~\frac{JA}{AK}\cdot\frac{KF}{FI}\cdot\frac{IN}{NJ}=1.
Перемножив эти три равенства и учитывая, что
ID\cdot IC=IE\cdot IF,~JB\cdot JA=JC\cdot JD,~KA\cdot KB=KF\cdot KE
(равенство произведений всей секущей на её внешнюю часть), получим:
1=\left(\frac{ID}{DJ}\cdot\frac{JL}{LK}\cdot\frac{KE}{EI}\right)\cdot\left(\frac{JB}{BK}\cdot\frac{KM}{MI}\cdot\frac{IC}{CJ}\right)\cdot\left(\frac{JA}{AK}\cdot\frac{KF}{FI}\cdot\frac{IN}{NJ}\right)=
=\left(\frac{ID\cdot IC}{IE\cdot IF}\right)\cdot\left(\frac{JB\cdot JA}{JC\cdot JD}\right)\cdot\left(\frac{KA\cdot KB}{KF\cdot KE}\right)\cdot\left(\frac{LJ}{LK}\cdot\frac{MK}{MI}\cdot\frac{IN}{NJ}\right)=
=1\cdot1\cdot1\cdot\frac{LJ}{LK}\cdot\frac{MK}{MI}\cdot\frac{IN}{NJ}=\frac{LJ}{LK}\cdot\frac{MK}{MI}\cdot\frac{IN}{NJ}.
Что и требовалось доказать.
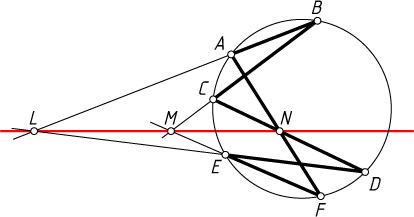
Примечание. Приведённое доказательство годится и для самопересекающегося шестиугольника (рис. 2), а также для шестиугольника, у которого две противоположные стороны параллельны (рис. 3): если противоположные стороны AB
и DE
вписанного шестиугольника ABCDEF
параллельны, прямые AF
и CD
пересекаются в точке P
, а прямые BC
и EF
— в точке Q
, то PQ\parallel AB
.
Прямая, содержащая точки L
, M
и N
, называется прямой Паскаля вписанного шестиугольника ABCDEF
.
Источник: Адамар Ж. Элементарная геометрия. — Ч. 1: Планиметрия. — М.: Учпедгиз, 1948. — с. 185-186
Источник: Пржевальский Е. Собрание геометрических теорем и задач. — М.: Типография Г. Лисснера и Д. Собко, 1909. — № 240, с. 97
Источник: Шклярский Д. О., Ченцов Н. Н., Яглом И. М. Избранные задачи и теоремы элементарной математики. — Ч. 2: Геометрия (планиметрия). — М.: ГТТИ, 1952. — № 129, с. 44
Источник: Прасолов В. В. Задачи по планиметрии. — Ч. 1. — М.: Наука, 1991. — № 6.92, с. 160
Источник: Прасолов В. В. Задачи по планиметрии. — 6-е изд. — М.: МЦНМО, 2007. — № 6.97, с. 161
Источник: Коксетер Г. С. М., Грейтцер С. Л. Новые встречи с геометрией. — М.: Наука, 1978. — с. 92

