16161. Дан треугольник ABC
, в котором \angle B=135^{\circ}-\frac{\alpha}{2}
и \angle C=45^{\circ}-\frac{\alpha}{2}
. Докажите, что:
а) центр E
окружности девяти точек треугольника ABC
лежит на стороне BC
;
б) если \angle A=60^{\circ}
, то AE
— биссектриса угла A
.
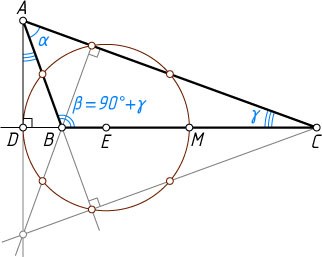
Решение. Пусть R
— радиус описанной окружности треугольника ABC
, AD
— высота, M
— середина стороны BC=a
. Обозначим углы при вершинах A
, B
и C
треугольника ABC
через \alpha
, \beta
и \gamma
соответственно.
а) Точки D
и M
лежат на окружности девяти точек треугольника ABC
, а радиус этой окружности равен \frac{R}{2}
(см. задачу 174). Поскольку
ED+EM=\frac{R}{2}+\frac{R}{2}\geqslant DM,
достаточно доказать, что DM=R
.
По условию
\beta=135^{\circ}-\frac{\alpha}{2},~\gamma=45^{\circ}-\frac{\alpha}{2},
поэтому
2\gamma=90^{\circ}-\alpha,~\beta=90^{\circ}+45^{\circ}-\frac{\alpha}{2}=90^{\circ}+\gamma\gt90^{\circ}.
Угол ABC
тупой, поэтому точка D
лежит на продолжении стороны BC
за точку B
(см. рис.). Значит,
\angle BAD=\angle ABC-\angle ADB=\beta-90^{\circ}=(90^{\circ}+\gamma)-90^{\circ}=\gamma.
По теореме синусов AB=2R\sin\gamma
, поэтому
DB=AB\sin\angle BAD=2R\sin\gamma\cdot\sin\gamma=2R\sin^{2}\gamma=R(1-\cos2\gamma)=
=R-R\cos2\gamma=R-R\cdot\cos(90^{\circ}-\alpha)=R-R\sin\alpha=R-\frac{a}{2},
откуда
DM=DB+BM=\left(R-\frac{a}{2}\right)+\frac{a}{2}=R.
Отсюда следует утверждение пункта а).
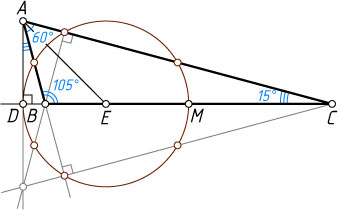
б) Если \alpha=60^{\circ}
, то
\gamma=45^{\circ}-\frac{\alpha}{2}=15^{\circ}.
Из треугольника ABD
получаем
AD=AB\cos\gamma=2R\sin\gamma\cos\gamma=R\sin2\gamma=R\sin30^{\circ}=\frac{1}{2}R=DE.
Тогда прямоугольный треугольник ADE
равнобедренный, поэтому
\angle DAE=45^{\circ}~\Rightarrow~\angle BAE=\angle DAE-\gamma=45^{\circ}-15^{\circ}=30^{\circ}=\frac{1}{2}\angle BAC.
Следовательно, AE
— биссектриса угла BAC
. Что и требовалось доказать.
Источник: Журнал «Crux Mathematicorum». — 2001, № 4, задача 2525 (2000, с. 177), с. 270

