16213. Точка D
лежит на стороне BC
треугольника ABC
, причём AD\gt BC
. Точка E
на стороне AC
такова, что
\frac{AE}{EC}=\frac{BD}{AD-BC}.
Докажите, что AD\gt BE
.
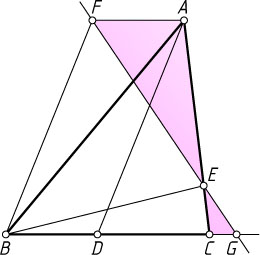
Решение. Достроим треугольник ADB
до параллелограмма ADBF
. Тогда FB=AD
и FA=BD
. Пусть G
— точка пересечения прямых FE
и BC
. Из подобия треугольников AEF
и CEG
получаем
\frac{FA}{CG}=\frac{AE}{EC}=\frac{BD}{AD-BC},
а так как FA=BD
, то
\frac{BD}{CG}=\frac{FA}{CG}=\frac{BD}{AD-BC},
откуда
CG=AD-BC~\Rightarrow~AD=BC+CG=BG.
Поскольку BEF
— внешний угол треугольника BEG
, а BF=AD
, то
BF=BG~\mbox{и}~\angle BEF\gt\angle BGE=\angle BGF=\angle BFE.
Тогда (см. задачу 3499) BF\gt BE
. Следовательно,
AD=BF\gt BE.
Источник: Польские математические олимпиады. — 1999
Источник: Журнал «Crux Mathematicorum». — 2004, № 5, задача 1 (2002, с. 130-131), с. 284
