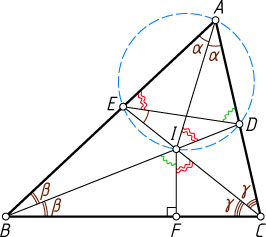
16225. В треугольнике ABC
проведены биссектрисы BD
и CE
, пересекающиеся в точке I
; F
— проекция точки I
на сторону BC
. Докажите, что если \angle ADE=\angle BIF
, то \angle AED=\angle CIF
.
Решение. Пусть углы треугольника ABC
, противолежащие сторонам BC
, CA
и AB
равны 2\alpha
, 2\beta
и 2\gamma
соответственно. Тогда
\alpha+\beta+\gamma=90^{\circ}.
По теореме о внешнем угле треугольника
\angle ADE=\angle CED+\angle DCE=\angle CED+\gamma,
а так как по условию
\angle ADE=\angle BIF=90^{\circ}-\angle FBI=90^{\circ}-\beta=(\alpha+\beta+\gamma)-\beta=\alpha+\gamma,
то \angle CED=\alpha
, т. е. \angle IED=\angle IAD
. Значит, точки A
, E
, I
и D
лежат на одной окружности (см. задачу 12). Тогда
\angle AED=\angle AID=\angle BAI+\angle ABI=\alpha+\beta=90^{\circ}-\gamma=\angle CIF.
Что и требовалось доказать.
Источник: Журнал «Crux Mathematicorum». — 2005, № 4, задача 2941 (2004, с. 229, 232), с. 246
