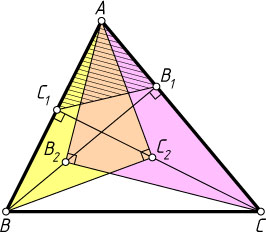
1632. На высотах BB_{1}
и CC_{1}
треугольника ABC
взяты точки B_{2}
и C_{2}
так, что \angle AB_{2}C=\angle AC_{2}B=90^{\circ}
. Докажите, что AB_{2}=AC_{2}
.
Указание. В прямоугольном треугольнике AB_{2}C
отрезок B_{2}B_{1}
— высота, проведённая из вершины прямого угла, поэтому AB^{2}_{2}=C\cdot AB_{1}
.
Решение. В прямоугольном треугольнике AB_{2}C
отрезок B_{2}B_{1}
— высота, проведённая из вершины прямого угла, поэтому AB^{2}_{2}=AC\cdot AB_{1}
. Аналогично AC^{2}_{2}=AB\cdot AC_{1}
.
Из подобия треугольников AB_{1}C_{1}
и ABC
(см. задачу 19) следует, что
\frac{AB_{1}}{AB}=\frac{AC_{1}}{AC},~\mbox{или}~AB_{1}\cdot AC=AC_{1}\cdot AB.
Поэтому AB^{2}_{2}=AC^{2}_{2}
. Следовательно, AB_{2}=AC_{2}
.
Примечание. Равенство AB_{2}=AC_{2}
можно доказать, не используя подобия. Ограничимся случаем \angle A=\alpha\lt90^{\circ}
Из прямоугольных треугольников AB_{1}B
и AC_{1}C
получаем
AB_{1}=AB\cos\alpha~\mbox{и}~AC_{1}=AC\cos\alpha.
Из прямоугольных треугольников AB_{2}C
и AC_{2}B
получаем
AB^{2}_{2}=AB_{1}\cdot AC=AB\cos\alpha\cdot AC~\mbox{и}~AB^{C}_{2}=AC_{1}\cdot AB=AC\cos\alpha\cdot AB.
Следовательно, AB_{2}=AC_{2}
.
Для \alpha\lt90^{\circ}
аналогично.
Источник: Зарубежные математические олимпиады. — 1976, Нью-Йорк
Источник: Конягин С. В. и др. Зарубежные математические олимпиады / Под ред. И. Н. Сергеева. — М.: Наука, 1987. — № 9.14, с. 32, Нью-Йорк, 1976
Источник: Прасолов В. В. Задачи по планиметрии. — 6-е изд. — М.: МЦНМО, 2007. — № 1.20, с. 13
