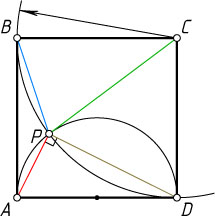
16331. Полуокружность с диаметром AD
на стороне квадрата ABCD
пересекается с окружностью с центром C
радиуса CD
в точке P
, отличной от D
. Докажите, что PB=AP\sqrt{2}
.
Решение. Точка P
лежит на полуокружности с диаметром AD
, поэтому \angle APD=90^{\circ}
. Значит,
PA^{2}+PD^{2}=AD^{2}.
Кроме того, PC=DC=AD
, а так как
PA^{2}+PC^{2}=PB^{2}+PD^{2}
(см. задачу 2169), то
PA^{2}+AD^{2}=PB^{2}+PD^{2}~\Rightarrow~PA^{2}+(PA^{2}+PD^{2})=PB^{2}+PD^{2}~\Rightarrow
\Rightarrow~2PA^{2}=PB^{2}.
Следовательно, PB=AP\sqrt{2}
. Что и требовалось доказать.
Источник: Журнал «Crux Mathematicorum». — 2013, № 5, задача 3745 (2012, с. 195, 196), с. 237
