16351. AD
, BE
и CF
— высоты остроугольного неравностороннего треугольника ABC
, H
— ортоцентр треугольника, а J
— ортоцентр треугольника DEF
(т. е. ортотреугольника треугольника ABC
). Докажите, что если \angle BAC=60^{\circ}
, то AJ\perp HJ
.
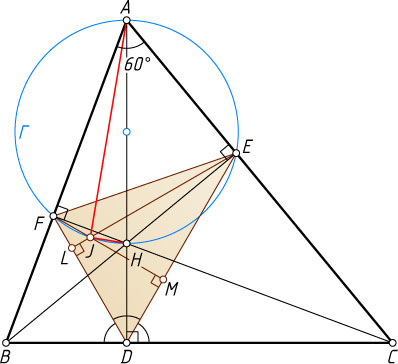
Решение. Рассмотрим случай, изображённый на рисунке.
Из точек E
и F
отрезок AH
виден под прямым углом, значит, эти точки лежат на окружности \Gamma
с диаметром AH
. Тогда
\angle EHF=180^{\circ}-\angle BAC=180^{\circ}-60^{\circ}=120^{\circ}.
Поскольку
\angle BDF=\angle BAC=60^{\circ}~\mbox{и}~\angle CDE=\angle CAB=60^{\circ}
(см. задачу 141), то
\angle EDF=180^{\circ}-60^{\circ}-60^{\circ}=60^{\circ},
Тогда
\angle EJF=\angle LJM=180^{\circ}-\angle EDF=180^{\circ}-60^{\circ}=120^{\circ}=\angle EHF,
где L
и M
— основания высот EL
и FM
треугольника DEF
. Значит, точка J
лежит на окружности \Gamma
, т. е. на окружности с диаметром AH
(см. задачу 12). Следовательно, \angle AJH=90^{\circ}
. Что и требовалось доказать.
Источник: Журнал «Crux Mathematicorum». — 2016, № 2, задача 4011, с. 79
