16388. Даны окружности \alpha
, \beta
и \gamma
радиусов a
, b
и c
с центрами A
, B
и C
соответственно. Окружность \gamma
касается окружностей \alpha
и \beta
в точках соответственно A'
и B'
, причём либо обеих внутренним образом, либо обеих внешним. Общая внешняя касательная окружностей \alpha
и \beta
касается их в точках S
и T
соответственно. Докажите, что:
а) прямые A'S
и B'T
пересекаются на окружности \gamma
;
б) A'B'^{2}=\frac{c^{2}\cdot ST^{2}}{(c\pm a)(c\pm b)}
, знак «+» соответствует внешнему касанию, а знак «-
» — внутреннему.
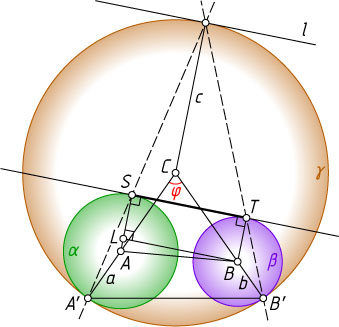
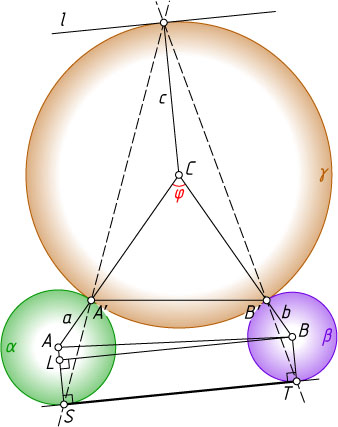
Решение. Рассмотрим случаи внутреннего и внешнего касания, изображённые на рис. 1 и рис. 2.
а) При гомотетии с центром A'
, переводящей окружность \alpha
в \gamma
, касательная ST
к окружности \alpha
перейдёт в касательную l
к окружности \gamma
, параллельную ST
, а при гомотетии с центром B'
, переводящей окружность \beta
в \gamma
, касательная ST
к окружности \beta
перейдёт в ту же касательную l
к окружности \gamma
. Значит, прямые A'S
и B'T
пересекаются на окружности \gamma
в точке касания прямой l
.
б) Рассмотрим случай внутреннего касания (рис. 1). Пусть F
— проекция точки S
на прямую BT
. По теореме Пифагора
AB^{2}=SF^{2}=ST^{2}+|SA-BT|^{2}=ST^{2}+(a-b)^{2}.
Обозначим \angle A'CB'=\varphi
. По теореме косинусов из треугольника ACB
получаем
\cos\varphi=\frac{CA^{2}+CB^{2}-AB^{2}}{2CA\cdot CB}~\Rightarrow
\Rightarrow~1-\cos\varphi=\frac{2CA\cdot CB-CA^{2}-CB^{2}+AB^{2}}{2CA\cdot CB}=\frac{AB^{2}-(CA-CB)^{2}}{2CA\cdot CB}=
=\frac{AB^{2}-((c-a)-(c-b))^{2}}{2CA\cdot CB}=\frac{AB^{2}-(c-b)^{2}}{2CA\cdot CB}.
Следовательно,
A'B'^{2}=2c^{2}(1-\cos\varphi)=c^{2}\cdot\frac{AB^{2}-(a-b)^{2}}{CA\cdot CB}=c^{2}\cdot\frac{ST^{2}+(a-b)^{2}-(a-b)^{2}}{CA\cdot CB}=
=c^{2}\cdot\frac{ST^{2}}{CA\cdot CB}=\frac{c^{2}\cdot ST^{2}}{(c-a)(a-b)}.
Для случая внешнего касания (рис. 2) аналогично получим, что
A'B'^{2}=\frac{c^{2}\cdot ST^{2}}{(c+a)(c+b)}.
Примечание. Из леммы Архимеда о сегменте (см. задачу 89) следует, что лучи A'S
и B'T
проходят через середину не содержащей точку A'
дуги окружности \gamma
. Отсюда вытекает утверждение а).
Источник: Журнал «Crux Mathematicorum». — 2021, № 2, задача 4566, с. 111

