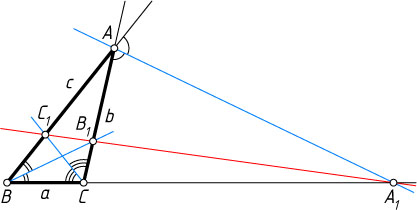
1639. Докажите, что биссектрисы двух внутренних углов неравнобедренного треугольника и биссектриса внешнего угла, не смежного с ними, пересекают прямые, содержащие противоположные этим углам стороны треугольника, в точках, лежащих на одной прямой.
Решение. Пусть биссектрисы внутренних углов при вершинах B
и C
треугольника ABC
пересекают стороны AC
и AB
в точках B_{1}
и C_{1}
соответственно, а биссектриса внешнего угла при вершине A
пересекает прямую BC
в точке A_{1}
.
Обозначим BC=a
, AC=b
, AB=c
. По свойству биссектрис внутренних и внешних углов треугольника
\frac{AC_{1}}{C_{1}B}=\frac{AC}{BC}=\frac{b}{a},~\frac{CB_{1}}{B_{1}A}=\frac{BC}{AB}=\frac{a}{c},~\frac{BA_{1}}{A_{1}C}=\frac{AB}{AC}=\frac{c}{b},
поэтому
\frac{AC_{1}}{C_{1}B}\cdot\frac{BA_{1}}{A_{1}C}\cdot\frac{CB_{1}}{B_{1}A}=\frac{b}{a}\cdot\frac{c}{b}\cdot\frac{a}{c}=1.
Следовательно, по теореме Менелая (см. задачу 1622) точки A_{1}
, B_{1}
и C_{1}
лежат на одной прямой.
Источник: Ефремовъ Д. Д. Новая геометрiя треугольника. — Одесса, 1902. — № 1, с. 23
Источник: Моденов П. С. Сборник задач по специальному курсу элементарной математики. — М.: Советская наука, 1957. — № 49, с. 186
Источник: Понарин Я. П. Элементарная геометрия. — Т. 1: Планиметрия, преобразования плоскости. — М.: МЦНМО, 2004. — № 10.1, с. 79
Источник: Прасолов В. В. Задачи по планиметрии. — 6-е изд. — М.: МЦНМО, 2007. — № 5.70б, с. 109
