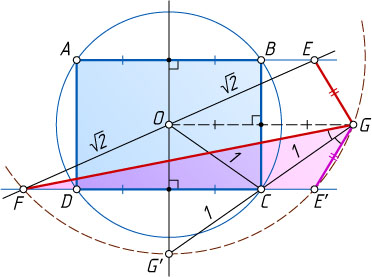
16401. В окружность радиуса 1 с центром O
вписан прямоугольник ABCD
. На луче AB
отметили точку E
, а на луче CD
— точку F
, причём OE=OF=\sqrt{2}
. Точка G
симметрична центру O
относительно стороны BC
. Найдите EG\cdot FG
.
Ответ. 2.
Решение. Очевидно, что точки E
и F
симметричны относительно O
, т. е. точки E
, O
, F
лежат на одной прямой.
Пусть точка E'
симметрична E
относительно прямой OG
, а точка G'
симметрична G
относительно C
. Заметим, что точка G'
лежит на серединном перпендикуляре к отрезку CD
, а точки F
и E'
симметричны относительно этого серединного перпендикуляра. Тогда
CG'=CG=OC=1,~OE'=OE=\sqrt{2},~FC=DE';
FC\cdot CE'=DE'\cdot CE'=(\sqrt{2}-1)(\sqrt{2}+1)=(\sqrt{2})^2-1^2=1
(см. задачу 2636). Значит, CG'\cdot CG=1=FC\cdot CE'
, и точки F
, G'
, E'
и G
лежат на одной окружности (см. задачу 114), причём G'
— середина дуги FE'
. Следовательно, GC
— биссектриса треугольника FGE'
. По формуле Лагранжа для длины биссектрисы (см. задачу 791) получаем:
EG\cdot FG=E'G\cdot FG=GC^2+FC\cdot CE'=1+1=2.