16434. Постройте прямоугольный треугольник по радиусам вписанной и описанной окружностей.
Решение. Пусть r
и R
— данные радиусы соответственно вписанной и описанной окружностей искомого прямоугольного треугольника.
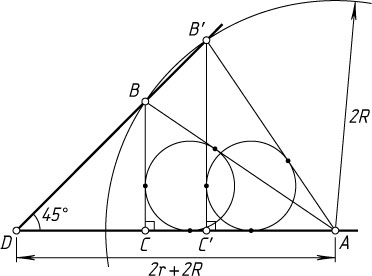
Построим угол с вершиной D
, равный 45^{\circ}
. Отложим на одной его стороне отрезок DA=2r+2R
. С центром в точке A
проведём окружность радиуса 2R
. Пусть она пересекает вторую сторону угла в точках B
и B'
. Опустим перпендикуляры BC
и B'C'
из точек B
и B'
на прямую AD
. Докажем, что ABC
(AB'C'
) — искомый треугольник.
Обозначим BC=a
, AC=b
и AB=2R=c
— диаметр описанной окружности треугольника ABC
. Пусть r'
— радиус вписанной окружности треугольника ABC
. Тогда по построению
a+b=BC+AC=DC+AC=2r+2R,
поэтому (см. задачу 217)
r'=\frac{a+b-c}{2}=\frac{(2r+2R)-2R}{2}=r.
Что и требовалось доказать.
Заметим, что треугольники AB'C'
и ABC
равны по гипотенузе и катету.
Задача имеет единственное решение (с точностью до равенства треугольников), если R\geqslant r(1+\sqrt{2})
(см. задачу 12863). В противном случае задача не имеет решений.
Гипотенуза искомого треугольника — c=2R
, а так как
a^{2}=c^{2}-b^{2}=4R^{2}-((2r+2R)-a)^{2},
то для a
(и b
) верно равенство
a=(r+R)\pm\sqrt{R^{2}-2rR-r^{2}}.
Источник: Журнал «Mathematics Magazine». — 1951, том 25, № 2, задача 99а, с. 112
