16440. Восстановите треугольник по центру O
его описанной окружности и основаниям D
и U
высоты и биссектрисы, проведённых из вершины A
.
Решение. Проведём окружность с диаметром OU
и окружность с центром U
и радиусом UD
. Пусть E
и E'
— точки пересечения этих окружностей. Проведём прямую EO
и касательную ко второй из построенных окружностей в точке D
. Пусть A
— точка пересечения этой касательной и прямой EO
.
Проведём окружность с центром O
и радиусом OA
. Пусть B
и C
— точки её пересечения с прямой DU
. Тогда ABC
— искомый треугольник. Аналогично точка E'
даёт второе решение — треугольник A'B'C'
.
Доказательство. По построению O
и D
— соответственно центр описанной окружности и основание высоты треугольника ABC
(и A'B'C'
). Поскольку
\angle AEU=\angle OEU=90^{\circ},
прямая AE
— касательная к окружности с центром U
и радиусом UD
. Прямоугольные треугольники ADU
и AEU
равны по катету и гипотенузе, поэтому AU
— биссектриса угла DAO
, а так как \angle BAD=\angle CAO
(см. задачу 20), то AU
— биссектриса угла BAC
(A'U
— биссектриса угла B'A'C'
).
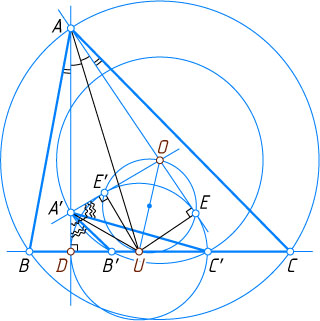
Источник: Журнал «Mathematics Magazine». — 1954, том 27, № 5, задача 183, с. 228
