16574. В остроугольном треугольнике ABC
высоты AH_{A}
, BH_{B}
и CH_{C}
пересекаются в точке H
. Через точки, в которых окружность радиуса HH_{A}
с центром H
пересекает отрезки BH
и CH
, проведена прямая l_{A}
. Аналогично проведены прямые l_{B}
и l_{C}
. Докажите, что точка пересечения высот треугольника, образованного прямыми l_{A}
, l_{B}
, l_{C}
, совпадает с центром окружности, вписанной в треугольник ABC
.
Решение. Покажем, что биссектрисы треугольника ABC
содержат высоты треугольника, образованного прямыми l_{A}
, l_{B}
, l_{C}
. Для этого достаточно доказать, что точка пересечения прямых l_{B}
и l_{C}
лежит на биссектрисе угла BAC
, а прямая l_{A}
перпендикулярна этой биссектрисе.
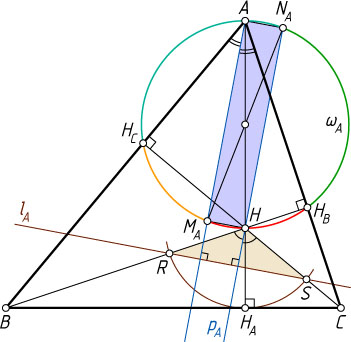
1) Пусть R
и S
— точки пересечения окружности с центром в H
радиуса HH_{A}
с отрезками BH
и CH
соответственно (рис. 1). Тогда треугольник RHS
равнобедренный с основанием RS
, поэтому прямая RS
(она же l_{A}
) перпендикулярна прямой p_{A}
, содержащей биссектрису угла BHC
(и H_{C}HH_{B}
). Поэтому достаточно доказать, что прямая p_{A}
параллельна биссектрисе угла BAC
.
Пусть M_{A}
и N_{A}
— середины дуг H_{C}HH_{B}
и H_{B}AH_{C}
окружности \omega_{A}
, построенной на AH
как на диаметре. Тогда (см. задачу 430) AM_{A}
— биссектриса угла BAC
, а HN_{A}
— биссектриса угла H_{C}HH_{B}
. Заметим также, что поскольку M_{A}N_{A}
— диаметр окружности \omega_{A}
, отрезки M_{A}N_{A}
и AH
пересекаются в центре окружности \omega_{A}
как её диаметры и делятся точкой пересечения пополам. Значит, четырёхугольник AM_{A}HN_{A}
— параллелограмм (даже прямоугольник). Следовательно, AM_{A}\parallel HN_{A}
, т. е. прямая p_{A}
параллельна биссектрисе угла BAC
. Что и требовалось.
2) Докажем, что прямые l_{B}
и l_{C}
пересекаются на биссектрисе угла BAC
.
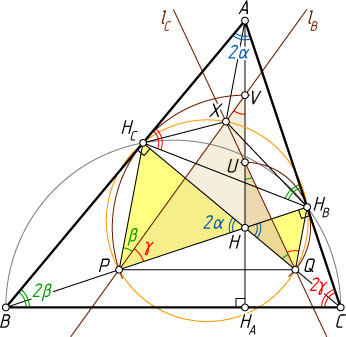
Пусть прямые l_{B}
и l_{C}
пересекают отрезки CH
и BH
в точках Q
и P
соответственно, X
— точка пересечения l_{B}
и l_{C}
(рис. 2), а углы при вершинах A
, B
и C
треугольника ABC
равны 2\alpha
, 2\beta
и 2\gamma
соответственно.
Поскольку HP=HH_{C}
и HQ=HH_{B}
, то треугольники HH_{C}P
и HH_{B}Q
— равнобедренные с углами, равными 2\alpha
при общей вершине H
. Поэтому
\angle HPH_{C}=\angle HQH_{B}=90^{\circ}-\alpha=\beta+\gamma.
Пусть прямые l_{B}
и l_{C}
пересекают отрезок AH
в точках U
и V
соответственно. Тогда треугольник PVH
равнобедренный с основанием PV
, значит,
\angle XPH=\angle VPH=\frac{180^{\circ}-\angle BHA}{2}=\frac{1}{2}\angle AHH_{B}=\frac{1}{2}\angle ACB=\gamma.
Рассуждая аналогично для треугольника QUH
, получаем, что \angle XQH=\beta
. Тогда
\angle XPH_{C}=\angle HPH_{C}-\angle HPX=(\beta+\gamma)-\gamma=\beta=\angle XQH_{C},
откуда следует, что точка X
лежит на окружности, описанной около треугольника H_{C}PQ
. Аналогично точка X
лежит на окружности, описанной около треугольника H_{B}PQ
. Таким образом, пять точек X
, H_{B}
, P
, Q
, H_{C}
лежат на одной окружности.
Тогда
\angle XH_{B}H_{C}=\angle XQH_{C}=\beta.
Четырёхугольник BH_{C}H_{B}C
вписанный, поскольку
\angle BH_{C}C=\angle BH_{B}C=90^{\circ}.
Значит,
\angle H_{C}H_{B}C=180^{\circ}-\angle ABC=180^{\circ}-2\beta,
т. е. \angle AH_{B}H_{C}=2\beta
, а так как \angle XH_{B}H_{C}=\beta
, то H_{B}X
— биссектриса угла AH_{B}H_{C}
. Аналогично, H_{C}X
— биссектриса угла AH_{C}H_{B}
. Тогда точка X
— центр окружности, вписанной в треугольник AH_{B}H_{C}
, а значит, лежит на биссектрисе угла BAC
.
Повторяя рассуждения пунктов 1) и 2) для двух других биссектрис треугольника ABC
, получаем, что точка пересечения биссектрис треугольника ABC
совпадает с точкой пересечения высот треугольника, образованного прямыми l_{A}
, l_{B}
, l_{C}
. Что и требовалось доказать.
Автор: Михайлов И. Н.
Источник: Московская математическая олимпиада. — 2024, LXXXVII, 11 класс, второй день, задача 4

