1742. Точка D
— середина гипотенузы AB
прямоугольного треугольника ABC
. Окружность, вписанная в треугольник ACD
, касается отрезка CD
в его середине. Найдите острые углы треугольника ABC
.
Ответ. 30^{\circ}
, 60^{\circ}
.
Указание. Треугольник ADC
— равносторонний.
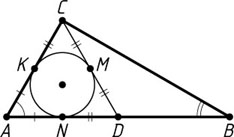
Решение. Пусть указанная окружность касается отрезка CD
в его середине M
, а отрезков AD
и AC
— в точках N
и K
соответственно. Поскольку медиана прямоугольного треугольника, проведённая из вершины прямого угла, равна половине гипотенузы (см. задачу 1109), то AD=CD
. По свойству касательных, проведённых к окружности из одной точки,
AK=AN,~CK=CM,~DN=DM=\frac{1}{2}CD=\frac{1}{2}AD,
поэтому AN=\frac{1}{2}AD
. Значит,
AC=AK+CK=AN+CM=\frac{1}{2}AD+\frac{1}{2}CD=CD=AD.
Поэтому треугольник ACD
— равносторонний. Следовательно,
\angle BAC=\angle DAC=60^{\circ},~\angle ABC=90^{\circ}-\angle BAC=30^{\circ}.
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 1.6, с. 10
Источник: Куланин Е. Д., Федин С. Н. Геометрия треугольника в задачах: Экспериментальное учебное пособие для 8—10 кл. школ физико-математического направления. — М.: НИИ школ, 1990. — № 37, с. 34
Источник: Московская математическая регата. — 2017-2018, первый тур, № 2, 8 класс
Источник: Математическая олимпиада МГУ «Ломоносов». — 2010-2011, заключительный этап, задача 5, 7-9 классы
Источник: Бегунц А. В., Бородин П. А., Горяшин Д. В. и др. Олимпиада школьников «Ломоносов» по математике (2005—2011). — М.: МЦНМО, 2011. — № 8.5, с. 103
