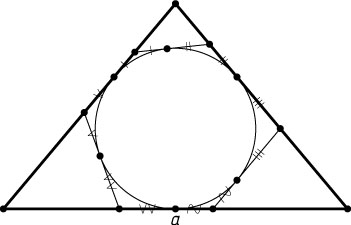
1751. В равнобедренный треугольник с основанием, равным a
, вписана окружность и к ней проведены три касательные так, что они отсекают от данного треугольника три маленьких треугольника, сумма периметров которых равна b
. Найдите боковую сторону данного треугольника.
Ответ. \frac{b-a}{2}
.
Указание. Примените теорему о равенстве отрезков касательных, проведённых к окружности из одной точки.
Решение. Сумма периметров отсечённых треугольников равна периметру данного треугольника (см. задачу 4623). Поэтому сумма боковых сторон равна b-a
. Тогда каждая боковая сторона равна \frac{b-a}{2}
.
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 11.8, с. 86
