1755. На основании AB
равнобедренного треугольника ABC
взята точка D
, причём BD-AD=4
. Найдите расстояние между точками, в которых окружности, вписанные в треугольники ACD
и BCD
, касаются отрезка CD
.
Ответ. 2.
Указание. Если окружность, вписанная в треугольник PQR
, касается стороны PQ
в точке S
, то PS=\frac{PQ+PR-RQ}{2}
(см. задачу 219).
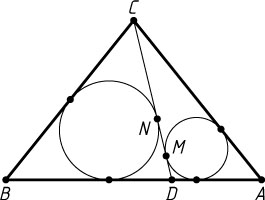
Решение. Пусть окружности, вписанные в треугольники ACD
и BCD
, касаются отрезка CD
в точках M
и N
соответственно. Поскольку AC=BC
, а
CM=\frac{AC+CD-AD}{2},~CN=\frac{BC+CD-BD}{2}
(см. задачу 219), то
MN=|CM-CN|=\left|\frac{AC+CD-AD}{2}-\frac{BC+CD-BD}{2}\right|=
=\frac{|BD-AD|}{2}=\frac{4}{2}=2.
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 11.30, с. 88
Источник: Гордин Р. К. ЕГЭ 2017. Математика. Геометрия. Стереометрия. Задача 14 (профильный уровень). — М.: МЦНМО, 2017. — № 3, с. 169
