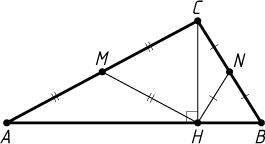
1805. Основание H
высоты CH
треугольника ABC
, проведённой из вершины наибольшего угла, соединили с серединами M
и N
сторон AC
и BC
. Докажите, что периметр четырёхугольника CMHN
равен сумме этих сторон.
Указание. HM=CM=\frac{1}{2}AC
, HN=CN=\frac{1}{2}BC
.
Решение. Поскольку угол C
— наибольший угол треугольника, точка H
лежит на стороне AB
(а не на её продолжении).
Медиана HM
прямоугольного треугольника ACH
равна половине его гипотенузы AC
(см. задачу 1109), т. е. HM=\frac{1}{2}AC
. Аналогично, HN=\frac{1}{2}BC
. Поэтому HM+HN=\frac{1}{2}(AC+BC)
. Следовательно,
HM+HN+CM+CN=\frac{1}{2}(AC+BC)+\frac{1}{2}(AC+BC)=AC+BC.
Источник: Гордин Р. К. ЕГЭ 2013. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2014. — № 1.30, с. 13
Источник: Гордин Р. К. ЕГЭ 2017. Математика. Геометрия. Стереометрия. Задача 14 (профильный уровень). — М.: МЦНМО, 2017. — № 1.30.1, с. 12
