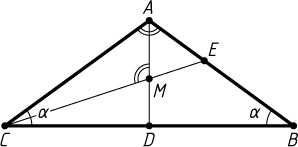
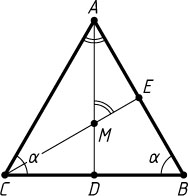
1807. Найдите углы равнобедренного треугольника, если известно, что угол между биссектрисой, проведённой из его вершины, и биссектрисой, проведённой к боковой стороне, равен углу при вершине.
Ответ. 36^{\circ}
, 36^{\circ}
, 108^{\circ}
или 60^{\circ}
, 60^{\circ}
, 60^{\circ}
.
Указание. Если угол треугольника равен \alpha
, то противолежащая сторона видна из точки пересечения биссектрис под углом 90^{\circ}+\frac{\alpha}{2}
.
Решение. Пусть угол при основании BC
равнобедренного треугольника ABC
равен \alpha
, а биссектрисы AD
и CE
пересекаются в точке M
. Тогда
\angle BAC=180^{\circ}-2\alpha.
Рассмотрим случай, когда \angle AMC=\angle BAC
. Поскольку
\angle AMC=90^{\circ}+\frac{1}{2}\angle ABC
(см. задачу 1101), то
90^{\circ}+\frac{1}{2}\alpha=180^{\circ}-2\alpha,
откуда находим, что \alpha=36^{\circ}
.
Если же \angle AME=\angle BAC
, то получим уравнение
90^{\circ}-\frac{1}{2}\alpha=180^{\circ}-2\alpha,
откуда \alpha=60^{\circ}
.
В первом случае углы треугольника ABC
равны 108^{\circ}
, 36^{\circ}
, 36^{\circ}
. Во втором случае треугольник ABC
— равносторонний.