1902. Серединные перпендикуляры к биссектрисам AA_{1}
, BB_{1}
и CC_{1}
треугольника ABC
пересекают прямые BC
, AC
и AB
в точках A_{2}
, B_{2}
и C_{2}
. Докажите, что точки A_{2}
, B_{2}
и C_{2}
лежат на одной прямой.
Указание. Примените свойство серединного перпендикуляра к отрезку и тригонометрическую форму теоремы Менелая (см. задачу 1756).
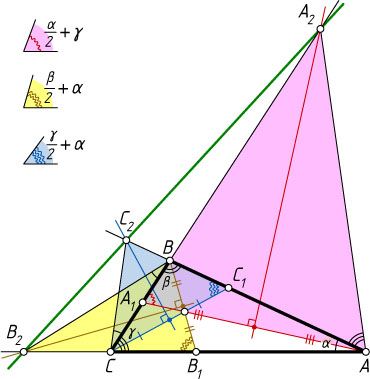
Решение. Рассмотрим случай, изображённый на рисунке. Обозначим \angle BAC=\alpha
, \angle ABC=\beta
, \angle ACB=\gamma
. Точка A_{2}
лежит на серединном перпендикуляре к отрезку AA_{1}
, значит, треугольник AA_{1}A_{2}
равнобедренный, поэтому
\angle A_{1}AA_{2}=\angle AA_{1}A_{2}=\frac{\alpha}{2}+\gamma
(AA_{1}A_{2}
— внешний угол треугольника AA_{1}C
). Тогда
\angle CAA_{2}=\angle A_{1}AA_{2}+\angle CAA_{1}=\frac{\alpha}{2}+\gamma+\frac{\alpha}{2}=\alpha+\gamma,
\sin\angle CAA_{2}=\sin(\alpha+\gamma)=\sin(180^{\circ}-\beta)=\sin\beta,
\angle BAA_{2}=\angle A_{1}AA_{2}-\angle BAA_{1}=\frac{\alpha}{2}+\gamma-\frac{\alpha}{2}=\gamma.
Аналогично
\angle ABB_{2}=\beta+\alpha,~\sin\angle CBB_{2}=\sin(180^{\circ}-\gamma)=\sin\gamma,~\angle CBB_{2}=\alpha,
\angle ACC_{2}=\gamma+\alpha,~\sin\angle ACC_{2}=\sin(180^{\circ}-\beta)=\sin\beta,~\angle BCC_{2}=\alpha.
Значит,
\frac{\sin\angle ACC_{2}}{\sin\angle C_{2}CB}\cdot\frac{\sin\angle BAA_{2}}{\sin\angle A_{2}AC}\cdot\frac{\sin\angle CBB_{2}}{\sin\angle B_{2}BA}=
=\frac{\sin\beta}{-{\sin\alpha}}\cdot\frac{-{\sin\gamma}}{\sin\beta}\cdot\frac{-{\sin\alpha}}{\sin\gamma}=-1.
Следовательно, по теореме Менелая в тригонометрической форме (см. задачу 1756) точки A_{2}
, B_{2}
и C_{2}
лежат на одной прямой. Аналогично для всех остальных случаев.
Источник: Понарин Я. П. Элементарная геометрия. — Т. 1: Планиметрия, преобразования плоскости. — М.: МЦНМО, 2004. — № 10.6, с. 79
